Вы не поняли чего-то. В тех примерах, на которые я ссылался, кривая Пеано строится как предел последовательности кривых. Эти кривые действительно содержат прямолинейные отрезки, которые проектируются в одноточечные множества, но при переходе к следующим кривым эти отрезки становятся всё короче и в пределе исчезают, так что никаких промежутков постоянства не остаётся.
Кроме того, количество отрезков постоянства может быть не более чем счётным, так как на каждом таком отрезке имеется рациональное число, а количество значений функции - несчётное (континуум), поэтому вовсе не каждому значению может соответствовать отрезок постоянства.
Далее буквы

будут обозначать целые числа, причём,
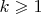
.
Построим непрерывную функцию
![$f\colon[0,1]\xrightarrow{\text{на}}[0,1]$ $f\colon[0,1]\xrightarrow{\text{на}}[0,1]$](https://dxdy-04.korotkov.co.uk/f/7/7/0/77060d9a64f702067da607dbee2f13de82.png)
, которая каждое своё значение принимает на множестве мощности континуум. Сначала определим функцию

Заметим, что эта функция непрерывна,

,

, на каждом отрезке
![$\left[\frac m3,\frac{m+1}3\right]$ $\left[\frac m3,\frac{m+1}3\right]$](https://dxdy-01.korotkov.co.uk/f/8/e/7/8e721bc45be535c2a40d9d7e2d5914f482.png)
,

, её можно записать в виде

или

, каждое своё значение на отрезке
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
она принимает более одного раза, причём, на каждом отрезке
![$\left[\frac m3,\frac{m+1}3\right]$ $\left[\frac m3,\frac{m+1}3\right]$](https://dxdy-01.korotkov.co.uk/f/8/e/7/8e721bc45be535c2a40d9d7e2d5914f482.png)
- только один раз.
Далее предположим, что для некоторого натурального

функция

на отрезке
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
уже построена. Предполагаем, что эта функция удовлетворяет следующим условиям:
1)

непрерывна на
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
,

и

, поэтому

отображает отрезок
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
на весь отрезок
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
;
2) на каждом отрезке
![$\left[\frac m{3\cdot 6^{k-1}},\frac{m+1}{3\cdot 6^{k-1}}\right]$ $\left[\frac m{3\cdot 6^{k-1}},\frac{m+1}{3\cdot 6^{k-1}}\right]$](https://dxdy-03.korotkov.co.uk/f/e/1/e/e1e07b4e9265c6c48dac30519e82d63b82.png)
,

, её можно записать в виде

или

; в частности, на этом отрезке

принимает каждое своё значение только один раз;
3) каждое своё значение на отрезке
![$\left[\frac m{6^{k-1}},\frac{m+1}{6^{k-1}}\right]$ $\left[\frac m{6^{k-1}},\frac{m+1}{6^{k-1}}\right]$](https://dxdy-01.korotkov.co.uk/f/8/1/e/81eb785a03a1a22e60c58b90985831df82.png)
,

, функция

принимает более одного раза; если

, то множество значений функции

на этом отрезке совпадает с множеством значений функции

;
4) если

, то

при

.
При

годится

.
Определим

на отрезке
![$\left[\frac m{6^k},\frac{m+1}{6^k}\right]$ $\left[\frac m{6^k},\frac{m+1}{6^k}\right]$](https://dxdy-01.korotkov.co.uk/f/8/1/1/811a028ef74918ef2bfae401637d566282.png)
,

, так:

Графики трёх первых функций показаны на рисунке (

- зелёный,

- красный,

- синий).
Заметим, что каждый отрезок
![$\left[\frac m{6^k},\frac{m+1}{6^k}\right]$ $\left[\frac m{6^k},\frac{m+1}{6^k}\right]$](https://dxdy-01.korotkov.co.uk/f/8/1/1/811a028ef74918ef2bfae401637d566282.png)
,

, содержится в том из отрезков
![$\left[\frac{m'}{3\cdot 6^{k-1}},\frac{m'+1}{3\cdot 6^{k-1}}\right]$ $\left[\frac{m'}{3\cdot 6^{k-1}},\frac{m'+1}{3\cdot 6^{k-1}}\right]$](https://dxdy-01.korotkov.co.uk/f/0/8/4/084be3cb176c1ac6a8ca044bf72f8ddd82.png)
,

, для которого

или

, поэтому

и

; из этих равенств и из непрерывности функции

следует непрерывность

. Далее,

,

, поэтому

отображает отрезок
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
на весь отрезок
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
. Таким образом, свойство 1) выполнено.
Свойства 2) и 4) выполняются по построению.
Свойство 3) следует из того, что

на отрезке
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
каждое своё значение принимает более одного раза.
Таким образом, все требуемые свойства выполнены, и можно продолжать построение дальше. В итоге получается бесконечная последовательность непрерывных функций

,

.
Пусть
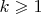
и
![$x\in[0,1]$ $x\in[0,1]$](https://dxdy-01.korotkov.co.uk/f/c/3/9/c3949c78998b68001ea9458772b3980b82.png)
. Почти очевидно, что

(немного подумав, можно заметить, что

). Поэтому при

будет

Отсюда по критерию Коши следует равномерная сходимость последовательности, и мы можем определить непрерывную функцию

,
![$x\in[0,1]$ $x\in[0,1]$](https://dxdy-01.korotkov.co.uk/f/c/3/9/c3949c78998b68001ea9458772b3980b82.png)
. Очевидно, что

и

, поэтому

отображает отрезок
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
на весь отрезок
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
.
Пусть
![$y_0\in[0,1]$ $y_0\in[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/d/9/ad94394ad4c80957eb8fb43feb38aff982.png)
. Можно проверить, что множество
![$f^{-1}(y_0)=\{x\in[0,1]:f(x)=y_0\}\neq\varnothing$ $f^{-1}(y_0)=\{x\in[0,1]:f(x)=y_0\}\neq\varnothing$](https://dxdy-02.korotkov.co.uk/f/d/3/6/d365ae1d0901449ba8bc8a025fe02e5f82.png)
не имеет изолированных точек, поэтому оно несчётно (имеет мощность континуума). Но мне уже не хочется это писать.



