Итак, Ферма утверждал, что уравнение

не имеет целочисленных решений при

. Попробуем доказать обратное.
1.1. Предположим, что такое решение существует, при

,

,

,
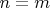
, где

,

,

- целые положительные взаимнопростые числа,

, пусть

,

- целое число >2.
Тогда

.
1.2.

, где

- целое положительное число.***

, где

-целое положительное число.***
1.3.

,

Перемножаем левые и правые части, получаем:

,

,

,

,

.***
1.4.

,

(п.1.1). Перемножаем левые и правые части, получаем:

, следовательно,

.
Левая часть равенства представляет собой значение функции

при

, а правая - при

, взятое с противоположным знаком.
Равенство будет выполняться в двух случаях:
1.4.1.если значение функции при

и

равно 0.
или 1.4.2.если функция в точках

и

принимает одинаковые значения разных знаков.
Рассмотрим каждый из случаев.
1.5.. Пусть

,

, тогда

,

, (

,

,

(п.1.3)), следовательно,

1.6. Исследуем функцию

.

,

,

-точка разрыва.
Найдем точки экстремума:


.

или

,

,

Так как на сегменте
![$]0;c]$ $]0;c]$](https://dxdy-02.korotkov.co.uk/f/1/6/c/16c732884e0dd3c035ebcffddad83d4d82.png)
существует только одна точка экстремума, первый вариант(1.4.1) невозможен.
2.1. Рассмотрим второй возможный вариант.
Функция

в точках

и

принимает одинаковые значения разных знаков. Она является целой рациональной функцией, непрерывна и определена при всех значениях

.Следовательно, между точками

и

найдется такая точка ( назовем ее

), что значение функции в этой точке будет равно

.



, т.к.

. Следовательно,
2.2.

,

, тк.

Тогда
2.3.

,

,

.
У меня тут мысль бредовая возникла: а может в связи со всем этим

? Если это так, то я распишу все для тройки сразу.
Решила расписать для

Итак, Ферма утверждал, что уравнение

не имеет целочисленных решений . Попробуем доказать обратное.
1.1. Предположим, что такое решение существует, при

,

,

, где

,

,

- целые положительные взаимнопростые числа,

, пусть

,
Тогда

.
1.2.

, где

- целое положительное число.***

, где

-целое положительное число.***
1.3.

,

Перемножаем левые и правые части, получаем:

,

,

,

,

.***
1.4.

,

(п.1.1). Перемножаем левые и правые части, получаем:

, следовательно,

.
Левая часть равенства представляет собой значение функции

при

, а правая - при

, взятое с противоположным знаком.
Равенство будет выполняться в двух случаях:
1.4.1.если значение функции при

и

равно 0.
или 1.4.2.если функция в точках

и

принимает одинаковые значения разных знаков.
Рассмотрим каждый из случаев.
1.5.. Пусть

,

, тогда

,

, (

,

,

(п.1.3)), следовательно,

1.6. Исследуем функцию

.

,

,

-точка разрыва.
Найдем точки экстремума:


.

или

,

,

Так как на сегменте
![$]0;c]$ $]0;c]$](https://dxdy-02.korotkov.co.uk/f/1/6/c/16c732884e0dd3c035ebcffddad83d4d82.png)
существует только одна точка экстремума, первый вариант(1.4.1) невозможен.
2.1. Рассмотрим второй возможный вариант.
Функция

в точках

и

принимает одинаковые значения разных знаков. Она является целой рациональной функцией, непрерывна и определена при всех значениях

.Следовательно, между точками

и

найдется такая точка ( назовем ее

), что значение функции в этой точке будет равно

и тогда

.



, т.к.

. Следовательно,
2.2




или

, отсюда

или

. Т.к.

, то

.
Тогда

,

, но это невозможно, т.к.

- рациональное число. Следовательно, второй вариант (1.4.2) также невозможен.
А раз оба варианта невозможны, уравнение

не имеет целочисленных решений.
Аналогично доказывается для всех других показателей
