ВТФ. Анализ одной идеи
Допустим (для определенности

не кратно простому

), что
1°)

, где

,

и, как известно, в базе

число

оканчивается на два нуля. Формулы для многочленов

и

хорошо известны и здесь не приводятся.
Введем числа
2a°)

и

,

;
2b°)

и

,

;
…
2t°)

и

,

,

.
3°) Число

, как легко видеть, делится на

, где
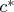
– наибольший (больше 1) общий делитель чисел

и

.
4°) Число

, как легко видеть, делится уже на

.
5°) Легко видеть, что с увеличением

отношения

,

и

(здесь

) стремятся к нулю.
Есть подозрение, что с какого-то момента с переходом к следующему

увеличение числа

становится меньше

(вернее – стремится к 1). И если это так, то с некоторого момента произведение всех

в числе

превысит ("задавит") само

.
Дело стоит за расчетом - теперь уже в поле действительных чисел.
Специалисты по пределам, что скажите вы?



