Изложенные выше соображения о “числовых” арифметических системах и арифметических системах “отношенческих” (или “реляционных”):
Хотя, почему, собственно, мы говорим о “системе положительных рациональных чисел”?
Ведь изначально так не было. Не было таких объектов, как “рациональные числа”. Изначально строго различались “числа” и “отношения”. Это были сущности двух разных типов (или сортов). И эта “парадигма” была очень авторитетна:
В свете вышеизложенного можно выразить мысль, что “полноценная” арифметика – это наука, скорее, об отношениях, чем о числах. А “предварительная” арифметика (арифметика “чисел”) становится полноценной только после погружения в поле своих отношений …
могут быть уточнены следующим образом. С позиций инь-ян философии:
 http://www.px-pict.com/10/4/2/1/3.htmlhttp://pogonn.h11.ru/Download/n4/Velikoe_protivostoanie.htmhttp://psi.lib.ru/filosof/iyrd.htmhttp://www.passion.ru/hor/fengshui/in.htmhttp://ru.wikipedia.org/wiki/%D0%AF%D0%BD%D1%8C
http://www.px-pict.com/10/4/2/1/3.htmlhttp://pogonn.h11.ru/Download/n4/Velikoe_protivostoanie.htmhttp://psi.lib.ru/filosof/iyrd.htmhttp://www.passion.ru/hor/fengshui/in.htmhttp://ru.wikipedia.org/wiki/%D0%AF%D0%BD%D1%8CИмеются:
Арифметическая числовая инь-система (односторонняя, несбалансированная):
,
где

– множество натуральных чисел, дополненное нулем (элементы этого множества будем называть “инь-числами”);

– обычная операция сложения на множестве

, которую будем называть “операцией инь-сложения”;

– обычная (частичная) операция вычитания на множестве

(когда можно вычитать только из большего меньшее или равное), которую будем называть “операцией инь-вычитания”;

– обычная операция умножения на множестве

, которую будем называть “операцией инь-умножения”;
индивидные константы

обозначают элементы

множества

.
-----------------
Арифметическая числовая ян-система (односторонняя, несбалансированная):
,
где

– множество аликвотных дробей, дополненное дробью

(элементы этого множества будем называть “ян-числами”);

–бинарная операция на множестве

, определяемая следующим образом:
если

и

, то

. Будем называть эту операцию “операцией ян-сложения”.

– (частичная) бинарная операция на множестве

, определяемая следующим образом:
если

и

и если

, то

. Будем называть эту операцию “операцией ян-вычитания” (согласно определению, производить ян-вычитание можно только из меньшего большее или равное).

– бинарная операция на множестве

, определяемая следующим образом:
если

и

, то

. Будем называть эту операцию “операцией ян-умножения”.
Индивидные константы

,

обозначают элементы

множества

.
-----------------
Арифметическая реляционная инь-ян-система (сбалансированная, гармоничная, уравновешенная):
,
где
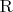
есть множество всех несократимых обыкновенных дробей вида

(

– натуральные числа), пополненное дробями вида

и

.

– бинарная операция на множестве
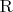
, определяемая следующим образом:
если

и

, то

. Будем называть эту операцию “операцией инь-сложения” (здесь и далее символ

обозначает унарную операцию приведения дроби к несократимому виду).

– бинарная операция на множестве
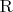
, определяемая следующим образом:
если

и

, то

. Будем называть эту операцию “операцией ян-сложения”.

– (частичная) бинарная операция на множестве
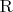
, определяемая следующим образом:
если

и

и если

, то

. Будем называть эту операцию “операцией инь-вычитания” (согласно определению, производить инь-вычитание можно только из большего меньшее или равное).

– (частичная) бинарная операция на множестве
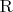
, определяемая следующим образом:
если

и

и если

, то

. Будем называть эту операцию “операцией ян-вычитания” (согласно определению, производить ян-вычитание можно только из меньшего большее или равное).

– бинарная операция на множестве
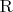
, определяемая следующим образом:
если

и

, то

. Будем называть эту операцию “операцией инь-ян-умножения”.
Индивидная константа

обозначает дробь

;
индивидная константа

обозначает дробь

;
Индивидная константа

обозначает дробь

.
--------------------
В арифметическую реляционную систему

весьма экономным образом “вложены” как арифметическая числовая инь-система

, так и арифметическая числовая ян-система

, обретающие внутри нее свое гармоничное сосуществование…




