Пример возрастающих последовательностей

,

,
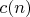
,

натуральных чисел, обладающих свойствами
1) ряд

сходится,
2) ряд

расходится,
3) ряд

расходится,
4) ряд

сходится.
Для удобства построений обозначим через

последовательность кружочков

, в которые будем вписывать
натуральные числа. Отрезком назовем конечное множество идущих подряд кружочков из

, а длиной отрезка -- количество содержащихся в нем кружочков.

разобъем на счетное множество непересекающихся отрезков:

. То есть, нечетные
отрезки будем обозначать

, а четные

.

имеет длину

,

имеет длину

.
Итак,

,

,

,

.
Определим последовательность

.
Обозначим объединение отрезков

и

через

. Отрезки

не пересекаются между собой и покрывают
все множество

. Отрезок

имеет длину

.
Заполним отрезки

натуральными числами, то есть, в кружочки впишем числа из

, так, что

заполнен последовательными натуральными числами, последнее из которых

. Проделав такую операцию для каждого

, получим последовательность

.
Запишем начало этой последовательности.

, соответствуют

.

, соответствуют

.
Теперь определим последовательности

и

.
Занумеруем все кружочки объединения отрезков

. Пусть некоторый кружочек при такой нумерации
имеет номер

, тогда число

равно номеру этого кружочка во множестве

.
Подобным образом получим последовательность

: занумеруем все кружочки из объединения отрезков

и положим

равным номеру кружочка во множестве

.
Начала этих последовательностей:

, соответствует отрезку

,

,

,

,

,

,

, соответствует отрезку

,

,

,

,

, соответствует отрезку

,


,

, соответствует отрезку

,

, соответствует отрезку

,

, соответствует отрезку

.
Последовательности

,

,

удовлетворяют условиям 1) и 2).
Построим последовательность
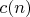
.
Обозначим объединение отрезков

и

через

,

.
Отрезки

не пересекаются между собой и покрывают множество

.
Отрезок

заполним последовательными натуральными числами, наибольшее из
которых

. Тогда все кружочки кроме первого окажутся заполнеными, а
получившуюся последовательность обозначим
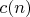
,

. Положим,

.
Построенные последовательности удовлетворяют всем четырем условиям.
Исследования сходимости рядов не привожу. Во всех четырех случаях его можно
провести при помощи оценок сумм, которые элементарны из-за монотонности.
Вопрос к Paata. Откуда выскочила такая интересная задача?



