МАТ
Уважаемый МАТ, попрошу Вас внимательно ознакомиться с предложенными выкладками и высказать свои суждения, замечания.
Ясно, что эта просьба относится и к другим участникам форума.
О прдставимости степеней натуральных чисел
суммами двух чисел в той же степени.
Обще известно, что при изучении сумм необходимо рассматривать только взаимно простые числа.
Сформулируем аксиому:
Сумма двух взаимно простых чисел взаимно проста с
каждым из слагаемых.

Если

взаимно просты, то и

взаимно просто и с

, и с

. Доказательство от противного. Предполагаем: пусть

не взаимно просто с

и имеет с ним общий множитель

, так что

а

. Тогда

Значит и

должно иметь множитель

т. е. быть не взаимно простым с числом

, что противоречит исходному.
Из этого следует, что если к сколь угодно составному числу прибавить единицу, или другое сколь угодно составное число, но с другими множителями, то в полученной сумме не окажется множителей, входящих в слагаемые.
КВАДРАТЫ.
Квадраты могут быть представлены суммой двух квадратов.
В этом утверждении ничего нового нет. Но метод, которым мы этого будем достигать отличается от известных и он нам понадобится в дальнейшем.
Из квадрата вычтем квадрат

. Разность

обозначим

, тогда

. Подставим это вместо


. И так разность квадратов представляется двояким образом. Это равносильные выражения.
Теперь задаемся вопросом: может ли разность квадратов быть равна квадрату? И для ответа на этот вопрос лучше подходит последнее выражение. Предположим

Тогда

. Анализируем
Слева четное число

, значит справа тоже должно быть четное число.

должно быть четным. Но, если

четно, то и

четно, и, наоборот, если не четны, то оба сомножителя . По этому, однозначно,

должно быть равно 2.

, тогда

. Тогда

. Тогда

. Слева

, справа

--это взаимно простые числа, поэтому

может принимать значения либо 1, либо 2.

, тогда

, тогда


, тогда

, тогда

.
А теперь остановимся и зададим себе такой вопрос: почему равенство

оказалось возможным, почему оно СОСТОЯЛОСЬ?! Оно состоялось потому, что слева только два сомножителя и ничто не мешает распределить между ними то, что находиться справа. Это очень важное утверждение. Здесь же добавим, что в этом равенстве можно левую и правую части умножить на любое (понятно одно и то же) число, от чего равенство сохраниться. Запишем

. Теперь числу

можно придавать значения

и т. д., и будем получать определенные значения

. И если эти значения подставить в

, то мы будем получать квадраты. И из этих же значений

состоит и


, квадрат которого представим суммой двух квадратов.
КУБЫ.
Куб не может быть представлен суммой двух кубов.
Из куба вычтем куб
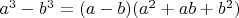
. Обозначим

. Тогда

. В неполный квадрат подставим это значение

.


. Предположим, что сумма этих 3-х слагаемых равна кубу.

. Тогда

.

и

это взаимно простые числа по любому простому числу

, кроме

(Смотри П4 на первой странице темы). Поэтому наличие числа 3 слева однозначно обязывает разность

быть равной 3 или

, где

. Пусть

. Подставим

. Далее запишем

.

. Число в скобке справа можно записать

. При любом

не содержащем 3, сумма этих двух слагаемых взаимно проста с

(смотри аксиому)
И так в равенстве

число

слева и число

справа взаимно просты, поэтому

может принимать значения либо 1, либо 3.
Если

, тогда

. Слева при любом

число четное, справа нечетное. Равенство не возможно.
Если

, тогда

,

. Слева при любом

четное, справа нечетное. Равенство не возможно. Сравниваем с квадратами и утверждаем, что здесь равенство не состоялось по той причине, что слева здесь три сомножителя

. И множитель

не позволил равенству состояться, о чем мы говорим с сожалением.
Но мы здесь обнаружили и то, что число

определенно должно быть равно 3, или

. Но что такое

? Это же

. Таким образом, если мы будем брать числа

и

такие, что

, то разность их кубов не может быть равна кубу.
А теперь рассмотрим случай, когда


, если

, то

. Подставим это значение

в равенство
![$a^3-b^3=3p[(b+3p)^2+(b+3p)b+b^2]=3p(b^2+6bp+9p^2+b^2+3bp+b^2)$ $a^3-b^3=3p[(b+3p)^2+(b+3p)b+b^2]=3p(b^2+6bp+9p^2+b^2+3bp+b^2)$](https://dxdy-01.korotkov.co.uk/f/4/0/7/407e12b9154e4cec6932a000cd278c3d82.png)
.
Окончательно запишем

. И задаемся тем же вопросом: может ли последнее выражение быть равно кубу?


. Слева есть множитель

, значит и справа должно быть множителю

и он должен быть и в

и в

. Положим

. Тогда

, и тогда

. И тогда запишем


. Поскольку

и

взаимно простые числа, то

в этом равентве может быть равно либо 1, либо 3. Если

, то

. Видим слева при любом

чет, справа нечет.
Если

то

. Слева чет, справа нечет. Таким образом равенство

невозможно. Это означает, что

кубу не равно.
Мы могли бы проделать аналогичные выкладки задавшись разностью

. Очевидно, что и в этом случае мы придем к такому же результату. Это означает, что разность

не может быть равна кубу, и мы вынуждены согласиться, что

не может быть равен сумме двух кубов.
5—ые СТЕПЕНИ.

a-b=c$

Подставим

или


. Но

. Произведение этих сомножителей должно содержать число 5, так как оно равно

. А это возможно если

, или

. Рассматриваем случай

, тогда

. Подставим это вместо

и после вычислений получим

.
Поскольку число

слева и число в скобке справа являются взаимно простыми числами (см. П4) , поэтому

может принимать значения либо 1 либо 5. И в том и другом случаях мы получим слева четное число, справа не четное. В точности так, как и у кубов. И поэтому мы можем сказать, что разность

, при

, пятой степени равно быть не может.
Рассмотрение случая, когда

приведет к тому же результату (как и у кубов), так что мы вынуждены согласиться, что и

невозможно записать суммой двух чисел в 5-ой степени.
7—ая СТЕПЕНЬ.
Если для 7—ых степеней проделать выкладки аналагичные кубам и 5-ой степ., то мы так же придем к равенству, у которого слева будет четное число, а справа нечетное и равенство не возможно. Таким образом и 7—ая степнь не представима суммой двух слагаемых в этой же степени. Из-за большой громоздскости выкладки я пока не привожу.
После сказанного становится понятным, что и для больших степеней

равных простым числам, окажется невозможным записать их суммой двух чисел в той же степени. А если такое правило присуще для простых показателей, то оно может быть рапространено и на составные числа, что обще известно.
Уважаемые участники форума, прошу внимательно рассмотреть предлагаемые обоснования с тем чтобы их или отклонить , или согласиться и отшлифовать.
С уважением Petern1.