Обращение ко всем участникам форума!
После трех месяцев работы форума на этой теме я могу сказать, что мои надежды не оправдались. Надежды на то, что и в наше время найдется еще много математиков, проявляющих интерес к НАУКЕ О ЦЕЛЫХ ЧИСЛАХ, или элементарной математике, как ее несправедливо сейчас называют. Лишь один Мат высказал поддержку, за что я ему благодарен.
И тем не менее я делаю еще одну попытку привлечь внимание к методам этой науки и предлагаю следующую задачу или теорему.
Доказать, что среди целых чисел можно найти сколь угодно много пар чисел—неквадратов! , но таких, сумма кубов которых равна сумме квадратов.

Обращение! Убедительно прошу, настоятельно рекомендую не читать мое доказательство, а попытаться решить эту задачу САМОСТОЯТЕЛЬНО. И тот кто этого достигнет испытает неописуемую радость и восхищение, ему откроются удивительные и прекрасные события во множестве целых чисел. И этот человек навсегда полюбит НАУКУ О ЦЕЛЫХ ЧИСЛАХ.
Я же приступаю к подробному изложению своего доказательства. Оговорюсь, что в доступной мне литературе такой теоремы я не встречал. Так что может быть это новое предложение.
Прежде всего отметим, что в этой задаче нет смысла рассматривать случай, когда

квадраты, так как

это настолько тривиально, что не интересно. Другое дело, когда

—неквадрат

—неквадрат. Однако, что мы знаем о сумме кубов? Что сумма кубов всегда равна произведению

и мы желаем, чтобы это произведение было равно сумме квадратов.

. Но что мы знаем о сумме квадратов? Мы доподлинно знаем, что если она равна произведению, то ее сомножители обязательно должны быть суммами квадратов. Это свойство сумм квадратов доказал Эйлер. Значит

должно быть равно сумме квадратов. Но мы только что сказали, что случай, когда

квадрат и

квадрат в нашей задаче рассмотрению не подлежат. Как будто противоречие. Выход из него такой. Надо взять два квадрата

и один квадрат увеличить на

единиц, а второй уменьшить на столько же. Тогда

--неквадрат

--неквадрат. Запишем
![$(a_0^2+l)^3+(b_0^2-l)^3=(a_0^2+b_0^2)[(a_0^2+l)^2-(a_0^2+l)(b_0^2-l)+(b_0^2-l)^2)]$ $(a_0^2+l)^3+(b_0^2-l)^3=(a_0^2+b_0^2)[(a_0^2+l)^2-(a_0^2+l)(b_0^2-l)+(b_0^2-l)^2)]$](https://dxdy-03.korotkov.co.uk/f/6/3/a/63a7fdc008fd215b6dd9dd64ddb79f6a82.png)
. Видим, что число в круглых скобках есть сумма квадратов и нам надо, чтобы и число в квадратных скобках было также суммой квадратов. Раскроем эти скобки, получим

.
Глядя на эти 6 слагаемых становиться грустно. Разве можно придумать, как из них сделать сумму из двух квадратов?
Побыв в растеренности вернемся к неполным квадратам

. Этим числам присуще свойство многозначности. Так что

, где

и

. Если в перечисленных равенствах вместо

подставлять

, то мы получим первый не полный квадрат разности. Так

. Этим мы доказываем верность сказанного о многозначности чисел

. Теперь в третьем числе вместо

подставим его значение

. Для дальнейшего движения последняя запись выгоднее, так как здесь сумма не трех, а двух слагаемых и один из них квадрат. У нас

тогда

. И нам надо, чтобы произведение

было квадратом. Раскроем скобки

. 4 слагаемых, три переменных и не видно ни какого пути как же нам находить при каких

эта сумма может быть равна квадрату. Опять тупиковая ситуация.
В таких ситуациях надо прибегать к математическим экспериментам или пробам.
Первая проба. Зададимся
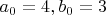


не сумма квадратов

не сумма квадратов

не сумма квадратов

Вторая проба. Пусть
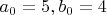

не сумма квадратов

не сумма квадратов

не сумма квадратов

. Немедленно замечаем, что в первой и во второй пробах мы получили числа, равные суммам квадратов при

. Делаем целевую проверку. Третья проба

.

Делаем предварительный вывод. При

и при различных

сумма

стабильно равна сумме квадратов. Почему же так? Вспоминаем. Ведь любая сумма квадратов есть число

, если

имеют разную четность, или есть число

, если

нечетны. Таким образом, суммы квадратов есть определенное количество 4, их

, плюс 1.
Мы же пытаемся в сумме

изменить слагаемые

да так, чтобы эта сумма не изменилась, да так, чтобы и число

, которое есть сумма квадратов, преобразовалось в новое число

, равное сумме квадратов. И эти условия как раз и определили то, что

. И это мы обнаружили, поведя эксперименты. Но минутку внимания. Мы же в этих опытах брали

пары последовательных чисел. Так что

. Тогда запишем
![$$(a_0^2-b_0^2+2l)^2+(a_0^2+l)(b_0^2-l)=[a_0^2-(a_0-1)^2+2l]^2+(a_0^2+l)[(a_0-1)^2-l]=(a_0^2-a_0^2+2a_0-1+8)^2+(a_0^2+4)(a_0^2-2a_0+1-4)=$$ $$(a_0^2-b_0^2+2l)^2+(a_0^2+l)(b_0^2-l)=[a_0^2-(a_0-1)^2+2l]^2+(a_0^2+l)[(a_0-1)^2-l]=(a_0^2-a_0^2+2a_0-1+8)^2+(a_0^2+4)(a_0^2-2a_0+1-4)=$$](https://dxdy-04.korotkov.co.uk/f/7/1/2/71223a359ebe456dd82ab20a27b4b28282.png)

.
Вот такое сложное выражение у нас получилось. Но мы не пугаемся. Мы не могли не заметить в наших опытах еще одну закономерность, что в получаемых суммах квадратов при

основания второго квадрата были:
Первый опыт

Второй опыт

Третий опыт

Таким образом, основание второго квадрата равно

. Квадрат этого числа будет
![$[a_0(a_0-1)-6]^2=a_0^4-2a_0^3-11a_0^2+12a_0+36$ $[a_0(a_0-1)-6]^2=a_0^4-2a_0^3-11a_0^2+12a_0+36$](https://dxdy-02.korotkov.co.uk/f/d/e/3/de370e9db254b3dccbf60bbe12099e2182.png)
. Если теперь это число, оно же квадрат, вычесть из сложного выражения, которое у нас получилось выше, то будем иметь

И так при

и при

получим
![$(a_0^2-b_0^2+8)^2+(a_0^2+4)(b_0^2-4)=(4a_0+1)^2+[a_0(a_0-1)-6]^2$ $(a_0^2-b_0^2+8)^2+(a_0^2+4)(b_0^2-4)=(4a_0+1)^2+[a_0(a_0-1)-6]^2$](https://dxdy-03.korotkov.co.uk/f/2/9/c/29c2489214d1d0ac01f23f897584b00f82.png)
. Теперь можно записать


. Далее
![$a^3+b^3=(a_0^2+4)^3+[(a_0-1)^2+4]^3=[a_0^2+(a_0-1)^2][(4a_0+1)^2+[a_0(a_0-1)-6]^2]$ $a^3+b^3=(a_0^2+4)^3+[(a_0-1)^2+4]^3=[a_0^2+(a_0-1)^2][(4a_0+1)^2+[a_0(a_0-1)-6]^2]$](https://dxdy-03.korotkov.co.uk/f/e/e/3/ee363fdd314a61dae095b6b1a08aaa9882.png)
. И так мы,наконец, получили произведение двух сумм квадратов, которое должно быть равно сумме квадратов. Для нахождения этой суммы квадратов применим формулы умножения сумм квадратов, которые приведены на первой странице темы. И получим
![$c=a_0(4a_0+1)+(a_0-1)[a_0(a_0-1)-6]$ $c=a_0(4a_0+1)+(a_0-1)[a_0(a_0-1)-6]$](https://dxdy-01.korotkov.co.uk/f/0/7/2/07299f3a896e22c7489258e1b2f2c83682.png)
![$d=(a_0-1)(4a_0+1)-a_0[a_0(a_0-1)-6]$ $d=(a_0-1)(4a_0+1)-a_0[a_0(a_0-1)-6]$](https://dxdy-04.korotkov.co.uk/f/f/6/e/f6ef3dbd8938479f68c82e8c7e13c05282.png)
. Или
![$c=a_0(4a_0+1)-(a_0-1)[a_0(a_0-1)-6]$ $c=a_0(4a_0+1)-(a_0-1)[a_0(a_0-1)-6]$](https://dxdy-03.korotkov.co.uk/f/6/0/6/606fbfe35f71f7fe0fb7d5055c917e8982.png)
![$d=(a_0-1)(4a_0+1)+a_0[a_0(a_0-1)-6]$ $d=(a_0-1)(4a_0+1)+a_0[a_0(a_0-1)-6]$](https://dxdy-02.korotkov.co.uk/f/1/a/9/1a9c4ca9214ec373ef11ff051bae861082.png)
. И запишем окончательный результат

. Словами скажем, что придавая

любые значения 1 , 2 , 3…и т. д. до бесконечности, мы будем получать

, сумма кубов которых будет равна сумме квадратов

. Но приведенными формулами охватываются не все возможные

, так как мы их получили только для

и

. Поэтому работа должна быть продолжена. Petern1.
Разбил очень длинную формулу на две строки. А также исправил четыре очевидных опечатки.
Petern1, следите, пожалуйста, за длиной строк, чтобы они помещались на экране. Jnrty


