Поздравляю, Вы доказали что в Меллеровской СО существует горизонт
...
Поэтому Ваш вывод о непринадлежности плоскости к пространству-времени не верен.
Вы ничего не поняли из того, что я
писал.
"Плоскость"

, которая в координатах

изображается прямой, не принадлежит пространству-времени Риндлера. На самом деле это пространство-время содержит только область

. Вторая область

с первой вообще никак не связана. Метрика

при

вырождается.
Не имеет никакого значения, как ведёт себя преобразование координат при  .
. Если сделать преобразование

то можно увидеть, что вся прямая

превращается в одну точку

. Метрика

нигде не вырождается и описывает геодезически полное пространство-время, поэтому есть основания считать, что именно она описывает истинный вид "плоскости"

. Заметьте, что ни одна изотропная или времениподобная геодезическая, начинающаяся внутри двух углов

, не проходит через точку

. Все эти геодезические покидают углы Риндлера через прямые

, которым не соответствуют никакие точки в пространстве-времени Риндлера.
Кстати, точно такая же ситуация с горизонтом чёрной дыры: то, что в координатах Шварцшильда изображается как "сфера"

, при переходе к координатам Крускала - Шекерса превращается в одну точку, через которую не проходит ни одна времениподобная или изотропная геодезическая, начинающаяся вне чёрной дыры.
Если речь здесь о
![$\[z^2 dt^2 - dz^2 \]$ $\[z^2 dt^2 - dz^2 \]$](https://dxdy-01.korotkov.co.uk/f/8/2/a/82ae0d296951d850329983bbc3fc9c9482.png)
, гравитации нет вообще, есть только корявое преобразование координат. Вы же сами об этом уже говорили!
Да, говорил. Но я не физик, а ОТО интересуюсь на уровне праздного любопытства. В данном вопросе я окончательно ещё не определился.
Munin в этом вопросе вроде бы поддерживает
eprosа и
VladTK, а я его воспринимаю как квалифицированного физика. Но мне кажется очень странным, когда мне заявляют, что гравитационное поле может появиться от того, что из пространства-времени Минковского вырезали какие-то куски и как-то их склеили. Ведь никаких изменений вдали от склейки не произошло.
Наверное, результат может имитировать "притяжение" к плоскости, но сама постановка задачи о статической гравитирующей плоскости вызывает у меня сомнения. В качестве аналогии приводят задачу из электростатики о заряженной плоскости, но физически эти задачи отличаются. Электрические заряды удерживаются на плоскости силами, которые не влияют на электрическое поле. В случае ОТО эти силы сами должны создавать гравитационное поле. Не факт, что при физически разумных предположениях плоскость может оставаться статической.
Ну, если не лень, можно проделать вычисления для случая плоского слоя конечной толщины.
Попробовал я прокрутить Вашу идею. Поскольку вычисление тензора Эйнштейна

у меня запрограммировано в пакете Mathematica, это не занимает много времени. Я взял Вашу сглаживающую функцию и получил в переходной зоне метрику

. Вычисление тензора Эйнштейна, который пропорционален тензору энергии-импульса, даёт

. Если Вы считаете, что анизотропное давление, не обращающееся в

на границе с пустым пространством, и при нулевой плотности энергии - это очень физично, то у меня нет слов.
Я также разобрался с решением Тауба для несжимаемой жидкости с плотностью

. Поскольку статья Тауба мне недоступна, пришлось считать самому (с помощью пакета Mathematica). Уравнения Эйнштейна для метрики

имеют вид

(специально написал уравнения без упрощений; штрих означает производную по

). Уравнение

, следующее из уравнений Эйнштейна, имеет вид

После тривиальных сокращений получаем

Вычитая третье уравнение из второго, получим

Все уравнения с точностью до обозначений совпадают с уравнениями, которые
написал Утундрий, поэтому есть надежда, что все они правильные.
Поскольку

предполагается постоянным, первое уравнение можно решить:

Видим, что в качестве независимой переменной лучше принять

Далее штрих будет обозначать производную по новой переменной

. Тогда уравнения примут вид

Из четвёртого уравнения, если его проинтегрировать как линейное относительно

, получим

а решение (1) с новой переменной примет вид
![$$e^{\mu}=C_1^2\sqrt[3]{\cos^4Z}\text{.}\eqno{(5)}$$ $$e^{\mu}=C_1^2\sqrt[3]{\cos^4Z}\text{.}\eqno{(5)}$$](https://dxdy-01.korotkov.co.uk/f/c/6/4/c640e7d0f05791d555d508c34506699e82.png)
Подставляя

и

из (4) и (5) в третье уравнение системы (3), можем найти оставшуюся функцию

. Если
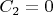
, то получим
![$$e^{\lambda}=C_3^2\frac{\sin^2Z}{\sqrt[3]{\cos^2Z}}\text{,}\eqno{(6)}$$ $$e^{\lambda}=C_3^2\frac{\sin^2Z}{\sqrt[3]{\cos^2Z}}\text{,}\eqno{(6)}$$](https://dxdy-01.korotkov.co.uk/f/4/6/7/46721beb510f975e46c4b8e4d3d19ad482.png)
что даёт вакуумное решение с космологической постоянной. Если же

, то будет
![$$e^{\frac{\lambda}2}=\frac{C_2}{\rho c^2}\left(1+\frac{|\sin Z|}{6\sqrt[3]{\cos Z}}\left(\mathbf B\left(\sin^2Z,\frac 12,\frac 16\right)+C_3\right)\right)\text{,}\eqno{(7)}$$ $$e^{\frac{\lambda}2}=\frac{C_2}{\rho c^2}\left(1+\frac{|\sin Z|}{6\sqrt[3]{\cos Z}}\left(\mathbf B\left(\sin^2Z,\frac 12,\frac 16\right)+C_3\right)\right)\text{,}\eqno{(7)}$$](https://dxdy-03.korotkov.co.uk/f/e/c/e/ece584b7fbddaeb65ee664c9c19fc57182.png)
где

есть неполная бета-функция (бета-функция

).
Подставляя (7) в (4), найдём
![$$p=\frac{\rho c^2|\sin Z|\left(\mathbf B\left(\sin^2Z,\frac 12,\frac 16\right)+C_3\right)}{6\sqrt[3]{\cos Z}+|\sin Z|\left(\mathbf B\left(\sin^2Z,\frac 12,\frac 16\right)+C_3\right)}\text{.}\eqno{(8)}$$ $$p=\frac{\rho c^2|\sin Z|\left(\mathbf B\left(\sin^2Z,\frac 12,\frac 16\right)+C_3\right)}{6\sqrt[3]{\cos Z}+|\sin Z|\left(\mathbf B\left(\sin^2Z,\frac 12,\frac 16\right)+C_3\right)}\text{.}\eqno{(8)}$$](https://dxdy-03.korotkov.co.uk/f/6/9/c/69c7dcf322df106e6532b958dd69592982.png)
Для возвращения к первоначальной переменной

нужно подставить в формулы (5) - (8) выражение (2).
Плоскостью симметрии решения является

. На этой плоскости

. Из выражения (5) видно, что

. Если

, то при возрастании

от

до

давление

возрастает до

. При

давление сначала убывает, становясь отрицательным, затем растёт до

. При

давление становится разрывным. В любом случае нарушается условие энергодоминантности

(кроме

, когда давление растёт только до нуля).
Как это применить к задаче о гравитирующей плоскости, не знаю. Хотелось бы иметь решение, симметричное относительно плоскости

, в котором давление положительно внутри слоя и равно

на границе с вакуумными областями, но, похоже, таких решений не существует. Между тем, если бы задача о статической гравитирующей плоскости была разумной, должно было бы существовать подходящее решение с постоянной плотностью хотя бы для достаточно тонкого слоя.
Поправка от 23/III-2009. С пределом давления в случае

наврал. Он на самом деле равен не

, а

. Поэтому в этом случае давление при

не растёт до нуля, а убывает до

.
Только не говорите мне, что при

имеем

и

.
Нет, конечно. Но компоненты тензора кривизны стремятся к нулю, так что пространство-время асимптотически плоское.
Как из кусочков Евклидовой плоскости можно склеить нечто, обладающее кривизной в местах склейки...
Не кривизной, а особенностями. Просто получается нечто не гладкое. Физическая осмысленность априори не ясна, поскольку при склейке должны выполняться определённые условия, которые здесь никто не проверял.
Не хотите говорить что за координаты - не надо.
Ну что Вы в позу становитесь.
Обсуждались здесь эти координаты.