Вот здесь почему бы Вам не объяснить что на что меняется?
Все на все меняется.
Первая же формула:
Цитата:
Рассмотрим консервативную голономную систему с энергией

и потенциальной энергией

. Тогда изменение её состояния происходит таким образом, чтобы

.
На каком множестве определена функция

?
Каковы пределы интегрирования?
Минимум чего и на каком множестве (и почему минимум)?
А если подкоренное выражение

?
что такое

?
В самом конце "доказательства" выясняется, что речь идет о материальной точке в силовом поле т.е. о втором законе Ньютона -- это тривиальный частный случай, если бы все остальное было адекватным.
В списке литературы из учебников по механике -- справочник по физике.
(Оффтоп)
Принцип Мопертюи -- один из вариационных принципов классической механики, который говорит, что траектории натуральной лагранжевой системы являются геодезическими некоторой римановой метрики, заданной в области конфигурационного многообразия.
Пусть на гладком многообразии

с локальными координатами

задана система с лагранжианом

где кинетическая энергия

является положительно определенной квадратичной формой обобщенных скоростей

, а

-- потенциальная энергия. Все функции мы считаем гладкими.
Зафиксируем константу интеграла энергии

и введем в области

риманову метрику формулой

. Эта метрика называется метрикой Якоби.
Теорема. 1) Пусть ![$x(t)\subset U_h,\quad t\in[t_1,t_2]$ $x(t)\subset U_h,\quad t\in[t_1,t_2]$](https://dxdy-04.korotkov.co.uk/f/f/5/7/f57111e350ef6c447c980d49f472d0bf82.png) -- решение уравнений Лагранжа с лагранжианом
-- решение уравнений Лагранжа с лагранжианом  и полной энергией
и полной энергией  . Тогда
. Тогда  является параметрическим уравнением геодезической метрики Якоби.
является параметрическим уравнением геодезической метрики Якоби.
2) Если параметризация геодезической ![$x=x(t)\subset U_h,\quad t\in[t_1,t_2]$ $x=x(t)\subset U_h,\quad t\in[t_1,t_2]$](https://dxdy-01.korotkov.co.uk/f/8/6/2/8628504e18f35076e29ac634e318d9ab82.png) метрики Якоби выбрана так, что
метрики Якоби выбрана так, что  удовлетворяет равенству
удовлетворяет равенству  при всех
при всех ![$t\in[t_1,t_2]$ $t\in[t_1,t_2]$](https://dxdy-04.korotkov.co.uk/f/3/6/7/367d8877163b88fa19378758cbe7adc682.png) , то
, то  является решением уравнений Лагранжа с Лагранжианом
является решением уравнений Лагранжа с Лагранжианом  Доказательство.
Доказательство. Проверим, что если функция

удовлетворяет равенству

, то она является решением уравнений Лагранжа с лагранжианом

тогда и только тогда, когда она является решением уравнений Лагранжа с лагранжианом

Действительно,

(каждый раз мы используем, что

)
и

Окончательно получаем
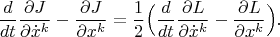
Теорема доказана.
Список литературы.С. Болотин, А. Карапетян, Е. Кугушев, Д. Трещев: Теоретическая механика. Москва, <<Академия>>, 2010.
А. Дубровин, С. П. Новиков, А. Т. Фоменко: Современная геометрия. Методы и приложения. Москва, <<Наука>>, 1986.



