Чтобы построить окружность, которая проходит через заданную точку

внутри угла

и при этом касается обоих его сторон

и

, можно воспользоваться следующим синтетическим приёмом с отражением.
## 1. Обозначения и цель* Пусть

— вершина угла.
* Лучи

и

— стороны угла.
* Точка

лежит строго внутри угла

.
* Надо найти центр

и радиус

такой, что:
1.

равноудалён от прямых

и

(т. е. окружность касается обеих сторон).
2.

(точка

лежит на окружности).
## 2. Построение1. **Проведите биссектрису** угла

.
Центр касательной окружности должен лежать на биссектрисе, поскольку только биссектриса обеспечивает равенство расстояний до прямых

и

.
2. **Отразите точку

** относительно одной из сторон угла, скажем,

.
* Опустите из

перпендикуляр на прямую

, отметьте проекцию

.
* Через

проведите перпендикуляр к

, и отложите на нём отрезок

в противоположную сторону от

. Получится точка

, отражение

относительно прямой

.
3. **Постройте серединный перпендикуляр** к отрезку
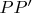
.
Любая точка на нём равноудалена от

и

, а потому её расстояние до

(половины перевёрнутого и исходного положения

) будет равно радиусу касательной.
4. **Найдите точку пересечения** биссектрисы

(шаг 1) и серединного перпендикуляра к
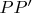
(шаг 3).
Обозначим это пересечение за

.
5. **Постройте окружность** с центром в

и радиусом

.
По построению:
*

равноудалён от

и

(касание обеих сторон).
*

расстояние от

до

— то есть окружность касается стороны

в точке, симметричной к

, и аналогично касается

.
## 3. Почему это работает* Центр

на биссектрисе гарантирует *одинаковое* расстояние до прямых

и

.
* Отражение точки

относительно

даёт точку

, для которой любая точка на серединном перпендикуляре к
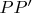
равноудалена от

и

. Но расстояние от любой такой точки до прямой

тоже равно

, что и есть радиус касания.
* Пересечение этих двух условий (на биссектрисе и на серединном перпендикуляре) даёт единственную точку

, удовлетворяющую одновременно и условию касания, и условию прохождения через

.
---
### Иллюстрация (схематично)
```
B
\
\
\ ← луч OB
\
\
C ← центр (на биссектрисе ℓ)
·
·|· ← серединный перпендикуляр к PP'
· | ·
· | ·
· | ·
P----+----P' ← отражение P относительно OA
\ |
\ |
\ |
\ |
\| ← луч OA
O
```
---
Таким образом, конструкция даёт требуемую окружность, касающуюся обеих сторон угла и проходящую через заданную точку внутри него.
, я так и не понял.



