Проверка способности ChatGPT решать математические задачи

[vicvolf]

realeugene в сообщении #1681551 писал(а):

А вы не пробовали в случае обнаружения ошибки запустить его снова на его же выдачу с просьбой найти ошибки?

Было и такое. Сначала запускал без режима DeepThink и находил ошибку. После этого копировал его ответ и просил проверить в режиме DeepThink и он находил ошибку, но не всегда. Если же находишь ошибку и ему говоришь об этом, то без режима DeepThink он сразу соглашается и делает исправления, а с режимом DeepThink он сначала проверяет твое замечание и если соглашается, то делает исправление. Интересно, что если ты задаешь необдуманный вопрос, который уже следует из того, что он ответил, то он игнорирует вопрос - вежливо говорит, что занят. Ко мне он уже привык и говорит со мной по-русски. Если просишь его сделать обзор статьи на английском, то он обдумывает ее на английском, а ответ выдает мне на русском, но обзор статьи он быстрее делает без режима - обдумывания (DeepThink).

[mihaild]

vicvolf в сообщении #1681557 писал(а):

Было и такое. Сначала запускал без режима DeepThink и находил ошибку. После этого копировал его ответ и просил проверить в режиме DeepThink и он находил ошибку, но не всегда.

Попробуйте скопировать ответ без ошибки и попросить найти ошибку - во многих случаях успешно найдет.

[realeugene]

Есть ещё один нюанс. Ответы нужно проверять в рамках другой сессии. ChatGPT по крайней мере утверждает, что не хранит информацию между сессиями. Модели обучены давать логичные ответы, поэтому, если один раз выдана ошибка, то велика вероятность, что она сохранится в рамках одной сессии.

Я только что полчаса пытался вывести ChatGPT на явную алогичность кучей последовательных вопросов, когда он отрицал существование некоторого механизма в некотором процессоре, потом сам нагуглил существование соответствующей инструкции, и только это его переубедило. При этом, про инструкцию он знал и детально рассказал мне, что именно она делает. И на вопрос про различие ответов объяснил, что пытается поддерживать логичность общения.

-- 09.04.2025, 14:30 --

mihaild в сообщении #1681560 писал(а):

Попробуйте скопировать ответ без ошибки и попросить найти ошибку - во многих случаях успешно найдет.

Ну так человек же лучше знает. Раз сказал, что там ошибка - значит, нужно искать. Поэтому важно ещё при формировании вопросов стараться не вносить собственные ошибки.

[mihaild]

realeugene в сообщении #1681567 писал(а):

И на вопрос про различие ответов объяснил, что пытается поддерживать логичность общения

Вот такие вопросы задавать модели бессмысленно. Это примерно то же самое, что спрашивать человека про активацию нейронов в его мозге.

[realeugene]

mihaild в сообщении #1681571 писал(а):

Вот такие вопросы задавать модели бессмысленно. Это примерно то же самое, что спрашивать человека про активацию нейронов в его мозге.

Не совсем: у модели есть закрытый от публики промпт, который задаёт её цели, но информацию о котором иногда можно получить из подобных обоснований. На самом деле, модель хочет про него рассказать, но его прямо рассказывать мешают явные инструкции в нём.

[mihaild]

realeugene в сообщении #1681572 писал(а):

На самом деле, модель хочет про него рассказать, но его прямо рассказывать мешают явные инструкции в нём

Получить этот промпт очень легко post1681285.html#p1681285.
А вот проследить связь ответов с конкретными кусками промпта модель не может.

[realeugene]

mihaild в сообщении #1681573 писал(а):

Получить этот промпт очень легко post1681285.html#p1681285 .

Не факт, что это настоящий промпт. Я скопировал этот вопрос на английском языке с просьбой напечатать всё в сессию, где был выдан один ответ на русском языке на мой вопрос на русском. Модель напечатала некоторый промпт на английском. После чего напечатала горизонтальную черту и свой ответ на первый вопрос, но в переводе на английский язык и без моего вопроса. То есть то, что она печатает в ответ на подобный вопрос, подвергается ещё какой-то обработке, которую модель считает более важной, чем мой вопрос про печатание промпта. Возможно, это вообще пасхалка.

На самом деле, понятно, что просто скопировать модель этот промпт не может, и он результат переосмысления промпта самой сеткой.

[Mihaylo]

Я работаю с Claude Sonnet 3.7, это типа самый крутой программист из всех LLM на сегодня.

В принципе он даёт кучу всяких советов, но они частенько не работают. Сегодня столкнулся с такой ситуёвиной: он мне говорит: "применяй такой-то метод, твой вариант будет плохо работать". Я послушался, но ничего не сработало. Короче, на сегодняшний момент, LLM-программисты очень сильно завязаны на stackoverflow и советы оттуда обожествляют. Я потом нагуглил, откуда интеллект это всё насобирал... Грубо говоря, уровень недоверия к stackoverflow отключен, и оттуда берутся все ответы как достоверные. В итоге LLM нашвыривает просто больше всяких разных версий, не проверяя их достоверность. Ибо это наша проблема, а LLM - молодцы.
А свою проблему, которую я решал, я прочитал в мануале, и там было написано, что мой метод рабочий, а предложенный ИИ способ ничем не лучше и не хуже. Просто чувак в стековерфлоу нагадил.

[mihaild]

realeugene в сообщении #1681576 писал(а):

На самом деле, понятно, что просто скопировать модель этот промпт не может, и он результат переосмысления промпта самой сеткой

Это, конечно, правда, но с простыми задачами "повторить текст" модели справляются достаточно надежно.

[realeugene]

mihaild в сообщении #1681623 писал(а):

но с простыми задачами "повторить текст" модели справляются достаточно надежно.

Пока им ничто не мешает. А публикации настоящего полного промпта разработчики яростно противодействуют. Так почему вы думаете, что промпт настоящий и достаточно полный, а не то, что вам позволили увидеть?

[Rasool]

Rasool в сообщении #1681002 писал(а):

Интересно, если задать эту задачу ChatGPT, то каков будет результат?

Вот ответ ChatGPT:

Цитата:

Основная идея заключается в том, что ходы первого игрока всегда перемещают камень вверх «на первую доступную свободную ступеньку» над ним. Делая такой ход, первый игрок «создает зазор» на более низком уровне. Выигрышная стратегия второго игрока заключается в том, чтобы всегда использовать свой ход для заполнения этого зазора, перемещая какой-либо камень (часто из нижней части блока камней) вниз на только что освободившееся место. При этом второй игрок не дает «базе» (то есть смежному блоку камней на самых нижних ступенях) расти вверх.
Можно показать (инвариантным аргументом или индукцией по n), что если второй игрок всегда «контратает», перемещая камень вниз, чтобы восстановить низкую конфигурацию, то в конечном итоге ни один камень никогда не будет продвинут достаточно высоко, чтобы достичь ступени 2n + 1.

[Rasool]

Задал ChatGPT задачу из вступительных задач в ЗФТШ по физике 1985-го года:

Цитата:

Спортсмены бегут колонной длины l по одному с одинаковой скоростью v. Навстречу бежит тренер со скоростью u меньше скорости v. Каждый спортсмен, поравнявшись с тренером, поворачивает и бежит назад с той же скоростью v. Какова будет длина колонны, когда все спортсмены развернутся?

Получил такое решение:

(Оффтоп)

**Решение задачи о колонне спортсменов**

Задача вроде классическая на относительное движение. Начнем с того, что спортсмены бегут в колонне длиной l. Каноничная ситуация, когда тренер бежит навстречу с меньшей скоростью, и каждый спортсмен разворачивается при встрече с ним. Важно, что каждый спортсмен возвращается с той же скоростью v, а тренер — с меньшей. После того, как все развернутся, длина колонны будет зависеть от всех этих факторов, и ключевыми станут время и скорость каждого участника.

**Рассматриваем движение спортсменов и тренера**

Спортсмены начинают бежать в положительном направлении с одинаковой скоростью. Тренер бежит навстречу с меньшей скоростью. Когда тренер встречает первого спортсмена, тот разворачивается и бежит назад. Тренер, тем временем, продолжает бежать в том же направлении, но с меньшей скоростью, поэтому он догоняет других спортсменов, один за другим. Мне нужно правильно учесть, как меняется расстояние между постоявшими спортсменами между каждым поворотом.

**Анализ движения спортсменов и тренера**

Тренер бежит назад, а спортсмены - вперёд. После встречи с тренером первый спортсмен разворачивается и бежит обратно, при этом тренер продолжает двигаться навстречу следующему спортсмену. Важно заметить, что спортсмены, разворачиваясь, продолжают увеличивать расстояние между собой. В конечном счёте, длина колонны будет расстоянием между первым и последним спортсменом к моменту, когда последний спортсмен развернется, встретив тренера.

**Определение длины колонны**

Мы хотим вычислить длину колонны спортсменов в момент, когда последний спортсмен встретится с тренером. Начальная позиция спортсменов — от x=0 в начале до x=-l на хвосте. Тренер стартует справа, бегая в левом направлении. Время встречи для каждого спортсмена зависит от скорости тренера и спортсмена. Таким образом, позиция первого и последнего спортсмена со временем изменяется, и длина колонны считается как разница между их положениями на момент встречи с тренером.


Думал на протяжении 22 секунд


Обознов?ем: первоначально спортсмены занимают отрезок длины $l$, бегут вправо со скоростью $v$. Тренер бежит навстречу (т. е. влево) со скоростью $u<v$. Как только очередной спортсмен встречает тренера, он тут же разворачивается и бежит влево со скоростью $v$.

1. Зафиксируем момент $t=0$, когда первый (передний) спортсмен встречается с тренером. Они оба в точке $x=0$. После этого:

* первый спортсмен идёт влево со скоростью $v$, его координата

$$ x_1(t) = -\,v\,t. $$

* тренер идёт влево со скоростью $u$, его координата

$$ x_{\rm coach}(t) = -\,u\,t. $$

* все ещё не встретившиеся со тренером спортсмены (в том числе последний) продолжают бежать вправо со скоростью $v$.

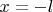
2. Последний спортсмен (который в момент $t=0$ был в точке $x=-l$) встретит тренера в тот же момент $t=T$, когда

$$ x_{\rm coach}(T)=x_{\rm tail}(T), $$

где

$$ x_{\rm tail}(T) = -\,l + v\,T, \qquad x_{\rm coach}(T) = -\,u\,T. $$

Отсюда

$$ -uT = -l + vT \;\;\Longrightarrow\;\; T\,(v+u)=l \;\;\Longrightarrow\;\; T=\frac{l}{v+u}\,. $$

3. В момент $t=T$ все спортсмены уже развернулись. Координаты «первого» (тот, кто повернул в $t=0$) и «последнего» (только что повернувшего) равны:

$$ x_1(T) = -v\,T = -\,\frac{v\,l}{v+u}, \qquad x_{\rm tail}(T) = -u\,T = -\,\frac{u\,l}{v+u}. $$

Расстояние между ними (длина колоны)

$$ l' = x_{\rm tail}(T)-x_1(T) = \Bigl(-\frac{u\,l}{v+u}\Bigr)-\Bigl(-\frac{v\,l}{v+u}\Bigr) = \frac{(v-u)\,l}{v+u}\,. $$

**Ответ:**

$$ \boxed{\,l'=\frac{v-u}{\,v+u\,}\;l\,.} $$

[A_I]

Rasool в сообщении #1685014 писал(а):

**Ответ:**

$$ \boxed{\,l'=\frac{v-u}{\,v+u\,}\;l\,.} $$

Лень проверять комплексно, но вот для некоторых граничных условий - при равных v и u очевидно, что колонна должна превратиться в шеренгу, чему, собственно, полученный ответ соответствует..
Ответ соответствует также и другим границам - $v > 0, u = 0$
В этом случае колонна останется той же длины..