Это понятно, но это доказательство в одну сторону(для того что бы ядро удовлетворяло этому соотношению достаточно что бы оно было таким, но не необходимо, другие варианты не исключены). Впрочем я наверное уже сильно докапываюсь там где не надо, это же задача по физике а не матанализу
Ну дык кто вам месшает возьмите оператор
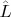
ядро

, и убедитесь, что
![$[\hat{L},\hat{x}]=0$ $[\hat{L},\hat{x}]=0$](https://dxdy-03.korotkov.co.uk/f/e/a/1/ea11c107e9d8eddde1a4db7c3e39e85282.png)
. И будет вам счапстье в втде необходимого условия. Да еще поколдуйте над явной записью

, с реализацией гильбертова пространства волновых функций

, с тем что бы ограничить класс возможных функций

ядра оператора , с тем что бы

. Правда в условиях задачи это врое нигде не написано, но вы разумно заметили, что надо какое-то ограничение на поведение f таки наложить
-- Вс апр 06, 2025 15:26:15 --Да, похоже с обобщенными ф-ми так в лоб нельзя. Надо с ними больше поработать
все шо нужно знать о дельта функцияx что

,кстати наверное можно было бы записать так
![$\boldsymbol\delta[f]=f(0)$ $\boldsymbol\delta[f]=f(0)$](https://dxdy-02.korotkov.co.uk/f/9/0/f/90f1ae9950cc196da28081233031b21f82.png)
-ибо дельта функция на самом деле функционал ... ну правило интегрирования по частям должно быть сохранено

, где f или из пространства финитных функций или пространства Шварца



