Телесный угол направлен от источника или к источнику ?

[Gleb1964]

Cosmochelik в сообщении #1676665 писал(а):

По идее = по логике, телесный угол должен быть направлен от точки из которой испускаються частицы, в точку(опираться на площадку), где мы их считаем, а не наоборот.
Мой вопрос в том, когда можно делать наоборот?

Вполне нормально считается наоборот.
Освещенность на поверхности, создаваемая элементарной площадкой источника, пропорциональна произведению яркости источника на телесный угол элемента и на косинус угла к нормали поверхности. В оптических системах сплошь и рядом так считается, есть готовые формулы для осесемметричного случая для центрированных оптических систем.

[Cosmochelik]

Gleb1964
Я заинтересовался этим, и решил найти все таки какой-то пример конкретного расчета.
В итоге нашел частичный ответ на мой вопрос у Сивухина



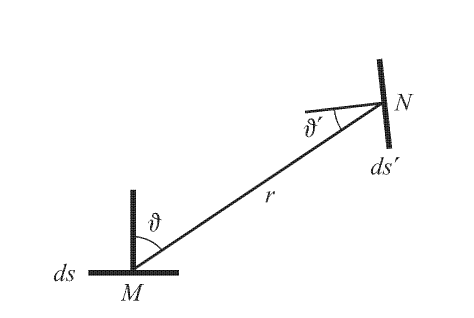
"Возьмем на поверхности источника бесконечно малую площадку $ds$. Пусть $ds'$ - освещаемая площадка, $ r $- расстояние между площадками, $\theta$ и $\theta'$ - углы составляемые нормалями к площадками с прямой NM, соединающей их. Телесный угол, под которым из площадки $ds$ видна площадка $ds'$, равен $ds' \cos \theta'/r^2$. В него площадка $ds$ посылает световой поток $d\Phi = B_{\theta}ds \cos \theta ds' \cos \theta' /r^2 $, или $d\Phi = B_{\theta}d\Omega ds' \cos \theta' $, где $d\Omega = ds \cos \theta /r^2$ - телесный угол под которым из освещаемой площадки $ds$' видна излучающая площадка $ds$. Разделив на $ds'$ найдем освещенность $dE$ площадки $ds'$, создаваемую потоком $d\Phi. $"

-- 28.02.2025, 13:02 --

Т.е. по определение там действительно нужно использовать угол от источника к приемнику.
Но было доказано, что при расчете можно делать и наоборот - от приемника к источнику. Более того - это намного удобней, ибо что-бы получить освещенность нужно делить на площадь приемника ds' - получается что для того что бы считать по первому методу нужно знать производную $\frac{ds}{ds'}$ (наверное).
Но как я понял, этот факт обеспечивает в доказательстве наличия косинуса в определении яркости: $L = \frac{d\Phi}{dS d\Omega \cos\theta}$ (кстати, а зачем он нужен ?). А если есть просто некая величина N, которая говорит лишь о том что у меня $dn$ частиц испускается в единицу времени $dt$ с площадки $dS$ т.е. $N = \frac{dn}{dt dS}$. И некий диск имеет эту постоянную величину N. Как найти кол-во частиц, проходящую через приемник площади $dS'$ в единицу времени ?

[Gleb1964]

Cosmochelik в сообщении #1676954 писал(а):

в определении яркости: $L = \frac{d\Phi}{dS d\Omega \cos\theta}$ (кстати, а зачем он нужен ?)

Косинус там уже не нужен, ведь там телесный угол площадки, как она уже видна с другой площадки. Косинус возникает когда используется площадь элементарной площадки и от нее считается ее видимый телесный угол.

[Cosmochelik]

Gleb1964
Я пытался понять, но не понял

[Gleb1964]

Нет, подумал, там косинус должен остаться, если свет падает на площадку под углом.

[Cosmochelik]

Ну ок. Ладно все равно спасибо, теперь понятно почему можно интегрировать по телесного углу который опирается на источник. Насчёт творого вопроса:

Cosmochelik в сообщении #1676954 писал(а):

А если есть просто некая величина N, которая говорит лишь о том что у меня $dn$ частиц испускается в единицу времени $dt$ с площадки $dS$ т.е. $N = \frac{dn}{dt dS}$. И некий диск имеет эту постоянную величину N. Как найти кол-во частиц, проходящую через приемник площади $dS'$ в единицу времени ?

То мне надо бы самому для начала найти конкретную формулировку задачи с ответом. Ибо именно этот косинус в определении яркости даёт возможность интегрировать по такому телесного углу. Поэтому завтра попробую что-то найти может не из оптики.