Вот еще покопался в библии:
Сивухин Д.В. Том 3. Электричество писал(а):
Уравнения Максвелла в интегральной форме справедливы и в тех случаях, когда существуют поверхности разрыва, на которых свойства среды или напряженности электрического и магнитного полей меняются скачкообразно. Поэтому в этой форме уравнения Максвелла обладают большей общностью, чем в дифференциальной форме, которая предполагает, что все величины в пространстве и во времени меняются непрерывно. Можно, однако, достигнуть полной математической эквивалентности обеих форм уравнений Максвелла. Для этого надо дифференциальные уравнения дополнить граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред.
Т.е. интегральные уравнения более общие чем дифференциальные, как отметил
УтундрийНо вот еще есть место:
Сивухин Д.В. Том 3. Электричество писал(а):
Правда, дифференциальная форма имеет смысл лишь в том случае, когда электричество распределено в пространстве с конечной плотностью

. Если

обращается в бесконечность в отдельных точках, на линиях или поверхностях, то дифференциальная форма становится неприменимой (С использованием так называемых обобщенных функций дифференциальную форму теоремы Гаусса можно распространить и на эти случаи.), тогда как интегральная форма применима и в таких случаях.
Т.е., полная эквивалентность достигается, если использовать обобщенные функции.
Если, например решать задачу на заряженную сферу обобщенными функциями, то получается, что мне не надо знать граничное условие на границе:
Рассмотрим случай равномерно заряженной сферической оболочки. Поле описывается дифференциальным уравнением:

где

--- радиус сферы. Сферическая симметрия задачи приводит к тому, что

, и поэтому:

Это обыкновенное дифференциальное уравнение, которое нужно решить. Для краткости обозначим

. Поскольку
неоднородность в правой части содержит дельта-функцию в точке

, и

, сделаем предположение:

Здесь

описывает поведение

для

, а

— для

. Обе функции

и
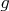
предполагаются гладкими.
Производная

теперь выражается как:

Упрощая, получаем:
![$$
E'(r) = f'(r) \theta(r - R) + \delta(r - R)[f(R) - g(R)] + g'(r) \theta(R - r).
$$ $$
E'(r) = f'(r) \theta(r - R) + \delta(r - R)[f(R) - g(R)] + g'(r) \theta(R - r).
$$](https://dxdy-03.korotkov.co.uk/f/6/0/2/602ebcd7db11e47e2bb58baa385ac64b82.png)
Подставляя это в дифференциальное уравнение, получаем:
![$$
[f'(r) + 2f(r)/r] \theta(r - R) + \delta(r - R)[f(R) - g(R)] + [g'(r) + 2g(r)/r] \theta(R - r) = C \delta(r - R).
$$ $$
[f'(r) + 2f(r)/r] \theta(r - R) + \delta(r - R)[f(R) - g(R)] + [g'(r) + 2g(r)/r] \theta(R - r) = C \delta(r - R).
$$](https://dxdy-01.korotkov.co.uk/f/4/a/5/4a52054bb0a84f8816700188dce5a65582.png)
Для выполнения этого уравнения необходимо выполнение трёх условий:

Для функций

и
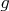
получаем одинаковую форму дифференциального уравнения, что приводит к одинаковому виду общего решения:
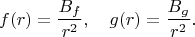
Для
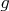
необходимо потребовать, чтобы

, чтобы избежать расходимости поля

в точке

. Теперь имеем

и

. Это означает, что:

откуда:

Получилось, что условие

вылезло автоматически. Но если решать без обобщенных, тогда действительно, мне надо знать, как сшивать решения и не обойдусь без граничных условий.