А если все-таки поискать?
Поищите, если есть желание.
-- 24.01.2025, 18:09 --Обоснование приведу позже.
Если кратко, модель бесконечного длинного соленоида противоречит четвертому уравнению Максвелла.
-- 24.01.2025, 18:21 --Подробнее.
Что мы знаем про эту модель?
У неё есть некий набор симметрий
1. Есть следующие симметрии для бесконечно длинного соленоида:
а) повороты вокруг

. Значит от угла

ничего не зависит.
б) трансляции вдоль

.
в) антисимметрия (направление

меняется на противоположное) при отражении относительно плоскости

Из которых выводится

для внешней области.
И, понятно, должны выполняться уравнения Максвелла.
Считаем, что токов нет, кроме как в самом соленоиде, зарядов нет.
Третье уравнение Максвелла в интегральной форме:

Пусть поток внутри соленоида меняется гармонически:

, а в качестве

выберем окружность в плоскости перпендикулярной оси соленоида с центром на оси. Тогда можно переписать так:
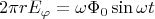
Поля же снаружи нет

Это вместе с

уже сразу противоречит четвертому уравнению Максвелла:
 -- 24.01.2025, 18:43 --
-- 24.01.2025, 18:43 --Но доведем до абсурда.

рассмотрим

-тую компоненту векторного уравнения:
С одной стороны,
![$$[\nabla \times \mathbf{B}]_\varphi = \frac{\partial B_r}{\partial z} - \frac{\partial B_z}{\partial r}$$ $$[\nabla \times \mathbf{B}]_\varphi = \frac{\partial B_r}{\partial z} - \frac{\partial B_z}{\partial r}$$](https://dxdy-03.korotkov.co.uk/f/2/e/e/2ee67e8bbd8925b139188f0919ad79db82.png)

- из трансляционной симметрии вдоль оси

С другой стороны,
![$$[\nabla \times \mathbf{B}]_\varphi = \mu_0 \varepsilon_0 \frac{\partial E_\varphi}{\partial t} $$ $$[\nabla \times \mathbf{B}]_\varphi = \mu_0 \varepsilon_0 \frac{\partial E_\varphi}{\partial t} $$](https://dxdy-02.korotkov.co.uk/f/9/5/7/957760b5b02ac2a5e2ef6dd96465062a82.png)
В результате:

И после интегрирования:

Мало того, что увеличивая частоту, мы можем сделать поле сколь угодно большим, так оно ещё и с расстоянием от соленоида падает медленнее, чем поле в цилиндрической волне

Конечно, этот результат ошибочен, но ошибка "заложена" в модели бесконечного соленоида.



