2*67#:
G19 len=15 len=16 len=17 len=18 len=19 len=20 len=21 len=22 average
v15: 1 1 1 17.00000000000000000000000000
G20 len=15 len=16 len=17 len=18 len=19 len=20 len=21 len=22 average
v15: 8 21 21 21 5 2 1 1 17.11250000000000000000000000
v16: 2 4 2 2 17.40000000000000000000000000
v17: 1 18.00000000000000000000000000
3*67#:
G19 len=15 len=16 len=17 len=18 len=19 len=20 len=21 len=22 average
v15: 1 1 18.50000000000000000000000000
G20 len=15 len=16 len=17 len=18 len=19 len=20 len=21 len=22 average
v15: 7 11 22 6 4 2 16.90384615384615384615384615
v16: 2 3 3 3 17.63636363636363636363636364
4*67#:
G19 len=15 len=16 len=17 len=18 len=19 len=20 len=21 len=22 average
v15: 1 16.00000000000000000000000000
G20 len=15 len=16 len=17 len=18 len=19 len=20 len=21 len=22 average
v15: 3 17 12 16 1 3 17.07692307692307692307692308
v16: 1 1 3 2 18.85714285714285714285714286
v17: 1 21.00000000000000000000000000
5*67#:
G19 len=15 len=16 len=17 len=18 len=19 len=20 len=21 len=22 average
v15: 1 16.00000000000000000000000000
v16: 1 19.00000000000000000000000000
G20 len=15 len=16 len=17 len=18 len=19 len=20 len=21 len=22 average
v15: 7 23 23 9 5 1 16.77941176470588235294117647
v16: 1 3 2 2 17.62500000000000000000000000
6*67#:
G19 len=15 len=16 len=17 len=18 len=19 len=20 len=21 len=22 average
v15: 1 1 16.00000000000000000000000000
G20 len=15 len=16 len=17 len=18 len=19 len=20 len=21 len=22 average
v15: 14 8 15 7 3 16.51063829787234042553191489
v16: 3 1 3 1 17.25000000000000000000000000
v17: 1 18.00000000000000000000000000
7*67#:
G19 len=15 len=16 len=17 len=18 len=19 len=20 len=21 len=22 average
v15: 1 1 15.50000000000000000000000000
G20 len=15 len=16 len=17 len=18 len=19 len=20 len=21 len=22 average
v15: 13 27 11 8 4 16.41269841269841269841269841
v16: 5 2 2 1 17.00000000000000000000000000
v17: 1 1 20.50000000000000000000000000
8*67#:
G19 len=15 len=16 len=17 len=18 len=19 len=20 len=21 len=22 average
v15: 1 1 17.50000000000000000000000000
G20 len=15 len=16 len=17 len=18 len=19 len=20 len=21 len=22 average
v15: 9 11 15 12 4 16.82352941176470588235294118
v16: 1 2 3 17.33333333333333333333333333
9*67#:
G19 len=15 len=16 len=17 len=18 len=19 len=20 len=21 len=22 average
v15: 1 1 19.00000000000000000000000000
G20 len=15 len=16 len=17 len=18 len=19 len=20 len=21 len=22 average
v15: 6 18 15 7 4 1 1 16.84615384615384615384615385
v16: 1 2 4 2 18.00000000000000000000000000
v17: 1 18.00000000000000000000000000



 , что даёт вероятность её обнаружения в данном диапазоне хуже 7 сигм или менее
, что даёт вероятность её обнаружения в данном диапазоне хуже 7 сигм или менее  ! Почти одна десятимиллиардная процента! И вот такая ничтожная вероятность реализовалась ...
! Почти одна десятимиллиардная процента! И вот такая ничтожная вероятность реализовалась ... 
![$\tikz[scale=.1]{
\fill[black] (0,0) rectangle (0.2,0.2);
\fill[black] (1,0) rectangle (2.1,1.1);
\fill (3,0) rectangle (6.4,3.4);
\fill (7,0) rectangle (14.3,7.3);
\fill (15,0) rectangle (28.1,13.1);
\fill (29,0) rectangle (47.7,18.7);
\fill (49,0) rectangle (71.9,22.9);
\fill (73,0) rectangle (95.85,22.85);
\fill (97,0) rectangle (115.8,18.8);
\fill (117,0) rectangle (129.9,12.9);
\fill (131,0) rectangle (137.9,6.9);
\fill (139,0) rectangle (141.5,2.5);
\node at (10.65,3.65)[white]{\textbf{22}};
\node at (21.55,6.55)[scale=2,white]{\textbf{23}};
\node at (38.35,9.35)[scale=3,white]{\textbf{24}};
\node at (60.45,11.45)[scale=4,white]{\textbf{25}};
\node at (84.425,11.425)[scale=4,white]{\textbf{26}};
\node at (106.4,9.4)[scale=3,white]{\textbf{27}};
\node at (123.45,6.45)[scale=2,white]{\textbf{28}};
\node at (134.45,3.45)[white]{\textbf{29}};
}
$ $\tikz[scale=.1]{
\fill[black] (0,0) rectangle (0.2,0.2);
\fill[black] (1,0) rectangle (2.1,1.1);
\fill (3,0) rectangle (6.4,3.4);
\fill (7,0) rectangle (14.3,7.3);
\fill (15,0) rectangle (28.1,13.1);
\fill (29,0) rectangle (47.7,18.7);
\fill (49,0) rectangle (71.9,22.9);
\fill (73,0) rectangle (95.85,22.85);
\fill (97,0) rectangle (115.8,18.8);
\fill (117,0) rectangle (129.9,12.9);
\fill (131,0) rectangle (137.9,6.9);
\fill (139,0) rectangle (141.5,2.5);
\node at (10.65,3.65)[white]{\textbf{22}};
\node at (21.55,6.55)[scale=2,white]{\textbf{23}};
\node at (38.35,9.35)[scale=3,white]{\textbf{24}};
\node at (60.45,11.45)[scale=4,white]{\textbf{25}};
\node at (84.425,11.425)[scale=4,white]{\textbf{26}};
\node at (106.4,9.4)[scale=3,white]{\textbf{27}};
\node at (123.45,6.45)[scale=2,white]{\textbf{28}};
\node at (134.45,3.45)[white]{\textbf{29}};
}
$](https://dxdy-02.korotkov.co.uk/f/1/3/2/132c758d4641045422be5848397bf00c82.png)
 суток. Или тысячу лет.
суток. Или тысячу лет. потому что 17-240 нашлась почти точно на
потому что 17-240 нашлась почти точно на  , а 15-228 около
, а 15-228 около 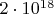 , а 13-192 около
, а 13-192 около  , а 11-168 около
, а 11-168 около  , видите, разница между 17-240 и 11-168 почти ровно 8 порядков или
, видите, разница между 17-240 и 11-168 почти ровно 8 порядков или  раз на единицу длины, и 19-252 ожидалась в
раз на единицу длины, и 19-252 ожидалась в  раза дальше 17-240 или около
раза дальше 17-240 или около  (плюс/минус разброс в пару-тройку раз). Именно такую оценку я где-то выше назвал первым более-менее приличным прогнозом.
(плюс/минус разброс в пару-тройку раз). Именно такую оценку я где-то выше назвал первым более-менее приличным прогнозом. . Ещё периодически возвращаюсь к старой идее об использовании симметрии и чтоб плясать не от начального числа кортежа, а от центрального.
. Ещё периодически возвращаюсь к старой идее об использовании симметрии и чтоб плясать не от начального числа кортежа, а от центрального. за вычетом простых до
за вычетом простых до  и усечённое на блок из 16 штук - для проверки делимости на AVX2.
и усечённое на блок из 16 штук - для проверки делимости на AVX2. матрицы не требует, выполняется медленными делениями начального числа, на скорость оно уже практически не влияет.
матрицы не требует, выполняется медленными делениями начального числа, на скорость оно уже практически не влияет. , это левые 12 столбцов матрицы, занимает всего 48 тактов на все 32 числа, или 1.5 такта на строку (кандидата), и это на 12 итераций, т.е. 8 чисел за один такт. А ведь проверка состоит из более десятка команд, но они все укладываются в 4 такта и более того, за эти 4 такта проверяют сразу 32 числа.
, это левые 12 столбцов матрицы, занимает всего 48 тактов на все 32 числа, или 1.5 такта на строку (кандидата), и это на 12 итераций, т.е. 8 чисел за один такт. А ведь проверка состоит из более десятка команд, но они все укладываются в 4 такта и более того, за эти 4 такта проверяют сразу 32 числа. полным-полно кортежей 17-240-1, порядка 2-х сотен. Неужто не очевидно, что в периоде
полным-полно кортежей 17-240-1, порядка 2-х сотен. Неужто не очевидно, что в периоде  их гораздо больше, порядка 3-х тысяч. И уже 10 из них известны.
их гораздо больше, порядка 3-х тысяч. И уже 10 из них известны.