Что такое определение?

[Sender]

Mihr в сообщении #1664465 писал(а):

Евгений Машеров в сообщении #1664428 писал(а):

Для начала - оно неверное.

Верное.

Минутку, вообще-то параллелограмм -- это четырёхугольник, у которого противоположные стороны параллельны. Есть множество четырёхугольников с равными противоположными сторонами, но далеко не все из них параллелограммы.

[Mihr]

Sender в сообщении #1664494 писал(а):

Есть множество четырёхугольников с равными противоположными сторонами, но далеко не все из них параллелограммы.

Можно пример такого четырёхугольника?

[Sender]

Каюсь, глупость ляпнул.

[katzenelenbogen]

Mihr в сообщении #1664495 писал(а):

Sender в сообщении #1664494 писал(а):

Есть множество четырёхугольников с равными противоположными сторонами, но далеко не все из них параллелограммы.

Можно пример такого четырёхугольника?

На обеих руках раздвиньте средний и указательный пальцы буквой V и приложите друг к другу пары концов пальцев разных рук так, чтобы плоскости пальцев разных рук были, допустим, перпендикулярны. Посмотрите на получившийся четырёхугольник из пальцев.

У него будут противолежащие стороны равны, но не параллельны.

-- 11.12.2024, 23:20 --

Mihr в сообщении #1664491 писал(а):

В общем, какими могут или какими должны быть определения - вопрос не вполне конкретный (и потому не вполне корректный). Тут нужно уточнять: для какой цели? Для начального знакомства с предметом? Или для совершенствования в нём? А может, ещё для чего-то? После формулировки цели разговор становится более предметным и ясным.

Для введения нового, ранее неизвестного и часто сложного слова (словосочетания) - для присвоения ему смысла, для раскрытия сути и разъяснения этого смысла.

Определение - это когда новому сложному слову присваивается значение.

Не может быть "определения предела по Коши и определения предела по Гейне". Потому что ты один раз присвоил значение слову. Второе утверждения вида "предел - это..." - это уже критерий являемости, это не присвоение слову значения, поскольку значение уже присвоено. Это не наполнение слова смыслом, поскольку смысл уже наполнен, когда давали "первое" определение.

[Mihr]

katzenelenbogen в сообщении #1664558 писал(а):

На обеих руках раздвиньте средний и указательный пальцы буквой V и приложите друг к другу пары концов пальцев разных рук так, чтобы плоскости пальцев разных рук были, допустим, перпендикулярны. Посмотрите на получившийся четырёхугольник из пальцев.

Вы по-своему понимаете слово "четырёхугольник". Насколько мне известно, четырёхугольник - это плоская фигура.

katzenelenbogen в сообщении #1664558 писал(а):

для присвоения ему смысла, для раскрытия сути и разъяснения этого смысла

Одна из характерных "болезней" начинающих обучение в вузе - поиск в определениях более глубокого смысла, нежели явно в них заложенный общеизвестный смысл. Пока Вы не избавитесь от этой привычки, будете нет-нет, да и спотыкаться на ровном месте. Не ищите скрытой "сути" в определениях, её там нет. Приучите себя к тому, что "суть" - понятие лишь философское, но не математическое. И даже не метаматематическое. Определения значат ровно то, что в них явно сказано. Больше ничего.

katzenelenbogen в сообщении #1664558 писал(а):

Не может быть "определения предела по Коши и определения предела по Гейне".

Ну, Вы же видели в учебнике эти два определения. Значит, может. И не просто может, а есть они, есть. Смиритесь с этим.

[EminentVictorians]

Mihr в сообщении #1664561 писал(а):

Одна из характерных "болезней" начинающих обучение в вузе - поиск в определениях более глубокого смысла, нежели явно в них заложенный общеизвестный смысл. Пока Вы не избавитесь от этой привычки, будете нет-нет, да и спотыкаться на ровном месте. Не ищите скрытой "сути" в определениях, её там нет. Приучите себя к тому, что "суть" - понятие лишь философское, но не математическое. И даже не метаматематическое. Определения значат ровно то, что в них явно сказано. Больше ничего.

Забавно, лично у меня ровно противоположное мнение)) И что суть в определниях есть (по крайней мере в некоторых), и что искать её - надо и полезно. И что метаматематический аспект из математики никуда не выкинешь. Может быть, конечно, я понимаю смысл слова "суть" не так как Вы, но не думаю, что дело только в этом.

[Mihr]

EminentVictorians в сообщении #1664563 писал(а):

Может быть, конечно, я понимаю смысл слова "суть" не так как Вы, но не думаю, что дело только в этом.

Вдумываться в определения с целью их усвоить - безусловно, полезно. Совершенно не полезно, однако, додумывать что-то "от себя", особенно пока ты ещё не ориентируешься в предмете. Этим страдают многие студенты (чаще - младшекурсники), и именно эта привычка "додумывания" обычно начинает выкидывать с её хозяином злые шутки. Полистайте любую тему из Пургатория (хоть М, хоть Ф) и убедитесь в том, что её автор всего лишь пытался "понять по-своему" то, что он (пока) понять не был способен. Вместо того, чтобы вдуматься в буквальное содержание учебника.
Посмотрите вот хотя бы на эту свежую тему: Первый замечательный предел и устранимый разрыв. Её автор - ни много, ни мало -

Innokenty Zholobov в сообщении #1664453 писал(а):

обнаружил изъян в нашей математической стройной теории

изучая понятие предела (точнее, "изучая" первый замечательный предел). Это он так "додумал" за автора учебника матанализа - доопределить по непрерывности функцию в точке устранимого разрыва - значит, локально, в отдельно взятой точке разрешить деление на ноль. Именно это его и "возмутило". То есть, то, что вызвало у него неприятие, - на самом деле его собственная фантазия. Но он приписывает её остальному миру и пытается этот самый мир "образумить". Поверьте, я много раз наблюдал нечто подобное. Проблема в подобных случаях всегда одна и та же - вместо того, чтобы внимательно вчитаться в определение, человек "вдумывается" в него, ищет в нём несуществующий смысл... А потом, "найдя" этот смысл, либо начинает его отстаивать, либо приписывает свою выдумку остальным, и начинает их "просвещать"... Я такое "проходил" уже бог знает сколько раз, поверьте.

[Booker48]

katzenelenbogen в сообщении #1664558 писал(а):

Не может быть "определения предела по Коши и определения предела по Гейне". Потому что ты один раз присвоил значение слову. Второе утверждения вида "предел - это..." - это уже критерий являемости, это не присвоение слову значения, поскольку значение уже присвоено. Это не наполнение слова смыслом, поскольку смысл уже наполнен, когда давали "первое" определение.

Тогда надо бы использовать первое зафиксированное определение предела (1655, Дж. Валлис):

Цитата:

Предел переменной величины — это величина постоянная, к которой переменная приближается так, что разность между ними может быть сделана меньше любой заданной величины

[Dan B-Yallay]

katzenelenbogen в сообщении #1664558 писал(а):

Не может быть "определения предела по Коши и определения предела по Гейне". Потому что ты один раз присвоил значение слову. Второе утверждения вида "предел - это..." - это уже критерий являемости, это не присвоение слову значения, поскольку значение уже присвоено.

katzenelenbogen в сообщении #1664425 писал(а):

Невозможно ввести новое слово, когда оно уже один раз введено. Определено.

Можете считать, что определение данное Коши относится к термину "предел по-Коши", а не к термину "предел вообще".
Аналогично с Гейне: "предел по-Гейне".

Например, с интегралами:
- Riemann integral
- Lebesgue integral
- Darboux integral
- Riemann–Stieltjes integral
- Lebesgue-Stieltjes integral
- Daniel integral
- Bochner integral
- Choquet integral
- Henstock–Kurzweil integral

[katzenelenbogen]

Dan B-Yallay
смотря в каком смысле.

Уважаемые коллеги. Честно говоря, хотелось бы обсудить главный вопрос, которому я посвятил тему и который сформулировал в первом посте, а не какие-либо второстепенные по отношению к этому основному вопросу вещи.

[EminentVictorians]

Mihr в сообщении #1664569 писал(а):

Вместо того, чтобы вдуматься в буквальное содержание учебника.

А есть ли оно, это буквальное содержание? Вот Вы приводили на прошлой странице определение $\mathbb R$ как непрерывного упорядоченного поля. Буквальное содержание - это то, что $\mathbb R$ - это непрерывное упорядоченное поле. Но исчерпывается ли оно своим буквальным содержанием? По-моему, нет. Есть огромные пласты информации, которые не видны, если воспринимать это определение просто как определение. Почему мы хотим именно поле? Что такое "непрерывное"? Полное по Дедекинду? А почему именно по Дедекинду, а не по Коши? А зачем нам линейный порядок? Может быть и частичного хватило бы? И так далее, вопросов миллион. И хоть Вы и говорите, что додумывать вредно, но лично мне так не кажется. Это же и есть творческий научный процесс. А давайте добавим в $\mathbb R$ бесконечно малое? Блин, потеряли полноту.. Можно ли восстановить? Нельзя. Но нужна ли нам полнота по Дедекинду? Вроде можно и без неё обойтись, если бы была полнота по Коши. Нужен ли линейный порядок? Наверное все же да. Я вот лично считаю, что так додумывать и крутить определения - это может быть суть математики и есть. Просто начинающие крутят не так профессионально как эксперты, но суть то одна и та же.


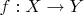
Что касается той темы про доопределение пределом. Там ведь тоже можно рациональное зерно найти. Это в нашей современной философской парадигме мы привыкли, что есть определения, теоремы, доказательства и т.д. Но даже относительно недавно тот же Эйлер, например, думал немного в другой парадигме. В современной математике бессмысленно ставить вопрос о том, чему равна функция $f:X \to Y$ в точке $z \notin X$. А ведь это было нормой не так и давно. Эйлер не смотрел, где определена функция $2^x$, он искал её значение в точке $\pi$ например (или $i$). То, что ТС-у кажется, что он обнаружил изъян в математической теории - так может быть этот изъян действительно есть. Да, мы привыкли мыслить в этой современной философской парадигме, что у функции есть область определения, что 0 в домен той функции не входит, что у неё есть конечный предел по базе проколотых окрестностей нуля, что её можно доопределить этим пределом до непрерывности. Это все понятно. Но стоит задуматься, а нормальная ли это вообще ситуация, когда язык таков, что нативное определение функции (в буквальном виде формулы $\frac{sin x}{x}$) рождает сущность с несвязной областью определения и вместе с этим однозначно доопределяемую до непрерывности в этой проблемной точке. Тогда как хорошая функция sinc требует для определения фигурную скобку и рассмотрение двух случаев. Может быть теоретико-множественный язык слишком сильный для матанализа?

[Dan B-Yallay]

katzenelenbogen в сообщении #1664578 писал(а):

смотря в каком смысле.

Поясните.

[Mihr]

EminentVictorians в сообщении #1664579 писал(а):

Просто начинающие крутят не так профессионально как эксперты, но суть то одна и та же.

Суть в том, что начинающий никогда не станет экспертом, если он с самого начала обучения считает себя таковым.

М. Боярский в роли д'Артаньяна писал(а):

Мне не нужны академии! Любой гасконец - с детства академик!

Подобного рода фразы и подобного рода настрой - хороши лишь для художественных фильмов (и не серьёзных, а исключительно развлекательных). Тот, кто на самом деле руководствуется ими в жизни, упускает свой шанс добиться чего-то реально значимого. Мне кажется, что все без исключения фрики - это те, кто изначально, ещё ничего собой не представляя, уже считали себя "не глупее автора" учебника и вместо того, чтобы всерьёз вдумываться в содержание изучаемого материала, начинали его по-своему "исправлять" в своём сознании. Примерно как рядовой Н. из анекдота. Который "Строевой Устав изучил и творчески переосмыслил".

Вот неплохая цитата в тему:

drzewo в сообщении #1653008 писал(а):

Постмодернизм принес в культуру идею о равноценности всех мнений. Почему эти идеи возникли именно в обществе потребления -- вопрос отдельный, однако, по счастью, все это не прижилось, инстинкт самосохранения и здравый смысл у человечества есть. Но некоторые, особо подверженные дурным влияниям личности, эту идею впитали -- всосали из телевизора.
В результате, всякая censored, нахватавшись где-нибудь и чего-нибудь, она не слушает плешивого в шапке, она дискутирует с ним <<на равных>>. Она, эта censored, не слушает и не учится, она высказывает свою точку зрения на предмет, потому, что как она усвоила, ее точка зрения равноценна тому, что говорит плешивый в шапке. В результате плешивый тратит время, а censored ничему не учится.

Но, похоже, этот спор бессмыслен: каждый из нас останется при своём мнении.

[Anton_Peplov]

katzenelenbogen
Рекомендую Вам прислушаться к этому совету.

Dan B-Yallay в сообщении #1664575 писал(а):

Можете считать, что определение данное Коши относится к термину "предел по-Коши", а не к термину "предел вообще".
Аналогично с Гейне: "предел по-Гейне".

Например, с интегралами:
- Riemann integral

- Lebesgue integral

- Darboux integral

- Riemann–Stieltjes integral

- Lebesgue-Stieltjes integral

- Daniel integral

- Bochner integral

- Choquet integral

- Henstock–Kurzweil integral

Считайте, что Коши и Гейне определили два понятия, еще не зная, что это одно и то же: "предел по Коши" и "предел по Гейне". (Да, математические понятия часто выражаются не одним словом, а сочетанием слов: "интеграл Римана" и "интеграл Лебега" - это разные вещи, словосочетание "линейное пространство" не разбивается на осмысленные части, и т.д.). А потом Вы доказали замечательную теорему, установившую, что это одно и то же понятие, и назвали его просто пределом. Какое из этих двух определений считать "настоящим" определением - вопрос вкуса. Я предпочитаю определение по Гейне за его общность: оно работает в произвольных топологических пространствах, в которых, вообще говоря, может не быть даже метрики.

[epros]

katzenelenbogen в сообщении #1664558 писал(а):

Не может быть "определения предела по Коши и определения предела по Гейне".

Вы неоднократно видели в учебниках, что может. И здесь Вам несколько раз сказали что может. И объяснили почему: потому что определение даётся словосочетанию, а не слову. Но Вы не желаете слышать. Я поражён.