Здравствуйте, впервые у вас. Пытаюсь изучать математику самостоятельно, в свободное от работы время, используя открытые ресурсы (в основном на английском языке, поскольку материала просто больше). Это пояснение было нужно.
Я правда хочу понять из каких соображений были выведены эти функции. Я имею ввиду, какие рассуждения могли к ним привести. Потому что во всех доказательствах, где бы я их не находил, везде эти функции почему-то даются как что-то самоочевидное и не требующее объяснений.
При этом сами по себе доказательства не сказать что очень сложны, время конечно потребовалось, но главная проблема из за которой я не удовлетворен этими доказательствами это полное отсутствие каких либо "оправданий" этим функциям.
Вот пара примеров:
На сайте OpenStax есть книга Calculus Volume 2. Доказательство теоремы Тейлора с остаточным членом в форме Лагранжа можно найти здесь:
Chapter 6.3, Theorem 6.7. Вспомогательная функция использующаяся в доказательстве имеет следующий вид:

Я вроде как понимаю, что

масштабирует остаточный член

когда мы изменяем

и это помогает нам в дальнейшем использовать теорему Ролля:

Но. Мы фиксируем

здесь, верно? Но почему мы не фиксируем

? Я имею ввиду, мы ведь обычно строим ряд Тейлора вокруг одной конкретной точки

(в данном случае

). Почему здесь мы фиксируем

и все время изменяем

которая по идее должна быть "центром"?
Я так же попытался это изобразить:
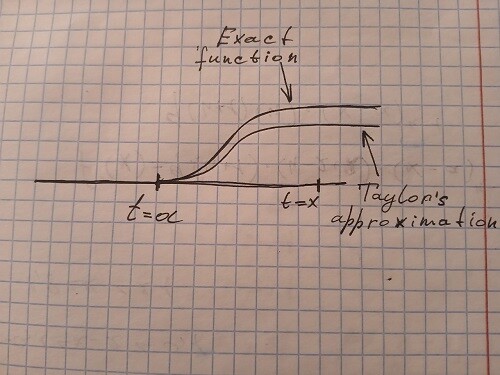
и я не понимаю, почему остаток должен исчезнуть при

, ведь расхождение там наоборот должно быть значительным.
Из каких соображений автор решил что вспомогательная функция

должна быть вот именно такой? Без каких либо объяснений это выглядит примерно следующим образом: "математик сидел, думал, разводил руками и внезапно понял что хочет чтобы функция была именно такой и вуаля, это сработало". Я прошу прощения.
Во втором примере то же самое:
В книге Principles of Mathematical Analysis (автор Walter Rudin) дается следующая функция (обвел красным):

В общем, как я уже сказал выше, я никак не могу понять "из какой шляпы" авторы из этих двух примеров достали эти вспомогательные функции. И без этого, все эти доказательства выглядят "искусственно".
Чтобы вы понимали мое отчаяние, лучшее объяснение которое я мог найти (на обоих языках) за долгое время поисков было приблизительно таким: "ну мы просто очень внимательно выбрали эту функцию, кто нам мешает это сделать? никто".
P.S.: надеюсь этот вопрос не нарушает правил dxdy.ru, так как он задан на половину на английском языке.



