Пусть у вас аффинное пространство

размерности

и ассоциированное векторное пространство

. Чтобы можно было говорить про ориентированный объём, достаточно зафиксировать единицу измерения этого самого объёма, то есть базис в старшей внешней степени

, которая одномерна. Заодно это вводит ориентацию на

и

. Можно такой базис вводить непосредственно, можно через скалярное произведение и ориентацию, можно через невырожденную симплектическую форму. А неориентированный объём соответствует уже скалярному произведению на

, то есть "базису с точностью до знака".
Кроме таких геометрических соображений, учтите, что группа ориентированных аффинных преобразований

, сохраняющих объём, — это

, она строго больше

при
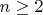
.



