Пусть существует путь (x(t),y(t)):

Рассмотрим
![$s = \sup\limits_{} t, t \in [0;1], x(t)=0. $ $s = \sup\limits_{} t, t \in [0;1], x(t)=0. $](https://dxdy-02.korotkov.co.uk/f/1/0/6/106f2bf3569656451a1e8a73bfdb945682.png)
. По непрерывности x(t) принимает все значения между 0 и а,
![$t \in [s;1]$ $t \in [s;1]$](https://dxdy-03.korotkov.co.uk/f/e/0/6/e06b0a82fbebef7e694d61ef3fb5c4de82.png)
. И можно подобрать такую последовательность

сходящуюся к s, что

сходится к 0, а

будет иметь два частичных предела -1 и 1. Что невозможно из-за непрерывности у(t).
Да, с линейной несвязностью всё так. Из этого и топологической связности следует, конечно, что ваше множество не локально линейно связно (в

). Более того, локально связные метризуемые компакты всегда локально линейно связны, так что ваше множество и не локально связно в той же точке.
Насчёт связности, вы начали с

. Далее делаете вывод, что

при некотором
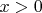
(если имело в виду, что при всех достаточно малых
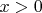
, то это из открытости

не следует). Потом стандартный аргумент показывает, что

содержит и все точки с большими абсциссами.