Если это читать буквально, как "из

следует
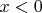
", то это просто неверно. Обычно вместо

ставят запятые, тогда такая запись означает, что

при

и

при
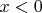
. То есть импликации в обратную сторону. И тогда не имеет особого значения, писать строгое или нестрогое неравенство, лишь бы все случаи (все значения

) были покрыты.
Ещё, если это именно определение, то надо всегда проверять, что разные случаи друг другу не противоречат. То есть в вашем первом примере формулы

и

дают одинаковое значение при

. Но конкретно модуль числа определяется в учебниках только по одному разу.