Треугольное число

, если кто не в курсе, есть

-ая сумма натурального ряда

Вопрос вырос из олимпиадной темы
https://dxdy.ru/topic146755.html, которая уперлась в уравнение

Задача с историей. "Хорошего" решения тут не найдено, есть перечень примеров, начиная с

Последнее описывает частную сумму последовательных кубов равную целому кубу:

Упомянутое уравнение можно записать еще так:

Дополним его четвертой переменной:

Равные суммы не равных последовательностей кубов. Тождество

для примера, описывает суммы

В обобщении некоторые вещи видны яснее, но как это решать? Перепишем

так:

и разделим почленно на

:

Соответствующее уравнение в рациональных числах имеет полное

-х параметрическое решение:

Обозначим модули выражений в скобках по порядку

Задача сводится к системе

Выразить каждую из пропорций отношением треугольных чисел — не проблема (об этом было
здесь), но ведь их бесконечная серия, причем не одна. А нужно с общим знаменателем

. Иногда это удается — для маленьких решений, добытых без того перебором кубов, но и только. Перебирать бесконечные серии, не имея уверенности в существовании решения как такового — удовольствие сомнительное. Домножить всё на "общий треугольный знаменатель" мешает немультипликативность функции

)) С другой стороны именно немультипликативность позволяет выразить любую рациональную точку отношением треугольников, с квадратами этот номер не проходит. Проблема требует локализации. Пойдем в обход. Как известно, тройка рациональных чисел выражается четырьмя целыми. Точнее, для заданной тройки
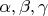
однозначно определены целые положительные

, не имеющие общего делителя

такие, что

Подставляя сюда треугольники, получаем

Это можно записать в строку:

Вот и причина. Отбросим кубы и связанную с ними задачу, далее всё в целых положительных числах. Вопрос следующий:
Известно, что существует бесконечно много пар треугольных чисел
пропорциональных двум фиксированным точкам числовой оси*.
Верно ли это для трех и более точек, и какие тут могут быть ограничения?Меня терзают смутные сомнения. Кажется, дело в больших числах. Даже для трех точек** рост треугольников должен быть значительный, а в задаче с кубами их четыре. Видим подножье горы.
В любом случае хороший повод для размышлений.
*
Если обе точки не являются целыми квадратами (upd 1.10.2021).**
Что соответствует уравнению  (upd 17.10.2021).
(upd 17.10.2021). 


