... т.е. отношение искомых переменных определено довольно точно.
Дробь

— вовсе не любая рациональная точка (отношение младших элементов пифагоровой тройки), но любая рациональная точка задает такую дробь* (функция от рациональной переменной):

где

Вот и попробуем свести неопределенности к минимуму, приравняв

Имеем уравнение

-й степени

Подставляя

получаем уравнение с целыми коэффициентами:

которое многое проясняет. Приближенные значения корня

задают примитивные тройки нужной пропорции, но искомые пифагоровы тройки не обязаны быть примитивными (из условия). Положим

и запишем условие так:

Отсюда

и

Чтобы радикал оказался рациональным числом, достаточно

(формула пошагового тестирования). Повторюсь, точные решения
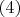
нам не нужны, даже если они есть. A нужны приближенные значения

из которых можно получить (по предположению) примитивные тройки, выдерживающие тест формулой

. Ну, а способ аппроксимации алгебраического числа описан
здесь. Пусть это будет самореклама. Очередное разложение. Да. Но по первому впечатлению такой поиск оказывается гораздо более "зрячий", поскольку остатки

быстро растут (как и положено для разложения

-й степени), и возможность "обратного скачка" связана с очень большим последующим знаком. Этим же объясняется отсутствие решений в больших номерах, и становится очевидной неразрешимость задачи для большинства

при случайном выборе. Несколько разложений для примера.



Тут вторая строка — знаки непрерывной дроби разложения корня

третья — соотв. подходящие дроби.





Тест:



Параметр

может оказаться рациональным числом, но не целым; с ростом величин часто так и происходит. Что ж, получаем тогда некоторые рациональные решения — не все, конечно, но "наименьшие".


Тест:



Общее впечатление такое, что исследуя случайные

, большей частью будем получать "ровную" дробь и отсутствие решений (что несколько удивительно), реже — рациональные решения (тут зависимость от количества целых делителей

) и совсем редко — целые решения. Последнее сопровождается "огромным" знаком цепной дроби и выявляет некое "очень точное" рациональное решение уравнения

Любые ли решения находятся таким способом — не знаю. Не уверен. Хвастаться пока нечем. Но интересно, какие еще задачи сводятся к разложению алгебраического числа? Похоже, тут непаханое поле.
*Задает, но двояко. Дело в том, что несократимые дроби

и

порождают одну и ту же пифагорову тройку.