Можно ли умножать комплексное число на действительное?

[epros]

EminentVictorians в сообщении #1604889 писал(а):

epros, а как у Вас определяется "подполе" и "изоморфны"?

Я уже говорил. В частности, что понимаю изоморфизм как биекцию, сохраняющую всю структуру.

EminentVictorians в сообщении #1604889 писал(а):

А у Вас множеств нету. Значит у Вас все эти вещи определяются как-то иначе.

Можете считать всё, что угодно, множествами, это вопрос подразумеваемой метатеории. Я уже говорил об этом. Мы ходим по кругу.

EminentVictorians в сообщении #1604889 писал(а):

И еще у меня иногда складывается впечатление, что Вы смешиваете изоморфизм и элементарную эквивалентность.

Нет.

mihaild в сообщении #1604867 писал(а):

Вообще, кажется, надо просто определять комплексные числа как набор $(X, \textcolor{green}{Y}, +_X, \cdot_X)$, где $(X, +_X, \cdot_X)$ - поле, $Y \subset X$ - его подполе, причем:
2) уравнение $x^2 +_X 1_X = 0_X$ разрешимо в $X$
3) $Y$ изоморфно $\mathbb R$ как полю
4) если $Z \subseteq X$ - подполе $X$, такое что $Y \subseteq Z$, и $x^2 +_X 1_X = 0_X$ разрешимо в $Z$, то $Z = X$

А зачем нужно уточнение "изоморфно $\mathbb R$ как полю"? Означает ли это, что $Y$ должно быть полем, но не обязательно непрерывным упорядоченным полем? Правильно ли я понял Вашу идею, что Вы, планируя построить модель $Y$ как $\mathbb{R} \times \{0\}$, хотите избавиться от наличия на нём порядка, унаследованного от $\mathbb{R}$, и всей прочей структуры, кроме структуры поля, унаследованной от той структуры поля, которую Вы построите на $\mathbb{R} \times \mathbb{R}$? Т.е. фактически Вам нужна только биективность $Y$ с $\mathbb{R}$?

Может быть я чего-то не понимаю, но мне кажется, что все эти исхищрения происходят из соображения, что $\mathbb{R}$ у нас "уже где-то есть, хотя и не внутри $\mathbb{C}$". По-моему, в аксиоматике достаточно ограничиться словами "содержит подполе $\mathbb{R}$". Ведь нам неважно, какова именно будет модель $\mathbb{R}$: будет ли это множество Дедекиндовых сечений, или это будет множество пар, в которых первый элемент - Дедекиндово сечение, а второй - нуль. Важно только, чтобы на этой модели соблюдалась вся аксиоматика действительных чисел. В таком случае вопрос топикстартера: "Можно ли умножать комплексное число на действительное", - естественным образом снимается, ибо в $\mathbb{C}$ содержатся сами действительные числа, не "нечто на них похожее".

[mihaild]

epros в сообщении #1604937 писал(а):

А зачем нужно уточнение "изоморфно $\mathbb R$ как полю"? Означает ли это, что $Y$ должно быть полем, но не обязательно непрерывным упорядоченным полем?

Потому что в этот момент я не хочу ничего говорить о порядке. Сложение и умножение на комплексных числах уже есть (раз это поле), значит их понятно как определять на $Y$. А больше ничего не понадобится.

epros в сообщении #1604937 писал(а):

Т.е. фактически Вам нужна только биективность $Y$ с $\mathbb{R}$?

Нет, мне еще нужно чтобы унаследованные $Y$ от $X$ сложение и умножение совпадали с порождаемыми биекцией.

epros в сообщении #1604937 писал(а):

По-моему, в аксиоматике достаточно ограничиться словами "содержит подполе $\mathbb{R}$"

По-моему нет. Потому что содержит много таких подполей.
Примерно как $n$-мерное векторное пространство - это такое, что в нём есть базис из $n$ векторов. Но выделенного базиса нет, поэтому чтобы говорить о координатах нужно его еще дополнительно зафиксировать.

-- 12.08.2023, 12:16 --

Пожалуй хорошая аналогия: можно ли умножать матрицы $n \times n$ на элементы $n$-мерного векторного пространства?

[Alexey Rodionov]

mihaild в сообщении #1604945 писал(а):

Пожалуй хорошая аналогия: можно ли умножать матрицы $n \times n$ на элементы $n$-мерного векторного пространства?

Провокация.

[mihaild]

Alexey Rodionov в сообщении #1604952 писал(а):

Провокация

Поясните.

[epros]

mihaild в сообщении #1604945 писал(а):

мне еще нужно чтобы унаследованные $Y$ от $X$ сложение и умножение совпадали с порождаемыми биекцией.

А зачем? Пусть не соответствует. Раз уж Вы решили определять $\mathbb{C}$ таким образом, чтобы оно включало не само $\mathbb{R}$, а нечто ему изоморфное, какая Вам разница, какие были сложение и умножение на $\mathbb{R}$?

mihaild в сообщении #1604945 писал(а):

По-моему нет. Потому что содержит много таких подполей.

Ну и что? "Таких" может быть и много, но само $\mathbb{R}$-то одно. Мы просто скажем про $\mathbb{R}$ в двух местах:
1) когда говорим про то, что $\mathbb{C}$ должно иметь его в качестве подполя и
2) когда говорим про то, что не существует строгого подполя $\mathbb{C}$, такого, что ...

mihaild в сообщении #1604945 писал(а):

Пожалуй хорошая аналогия: можно ли умножать матрицы $n \times n$ на элементы $n$-мерного векторного пространства?

Мне эта аналогия не кажется подходящей, поскольку матрицы $n \times n$ и $n$-мерные векторы принадлежат непересекающимся классам, в то время как действительные числа - подмножество комплексных и они перемножаются по правилам одного поля.

[EminentVictorians]

epros в сообщении #1604937 писал(а):

В частности, что понимаю изоморфизм как биекцию, сохраняющую всю структуру.

И Вы утверждаете, что можно говорить о биекции, не говоря о множествах?

-- 12.08.2023, 18:54 --

(Если что, я даже готов в какой-то степени согласиться, что так можно, но все равно хотелось бы услышать прямой ответ.)

[epros]

EminentVictorians в сообщении #1604969 писал(а):

И Вы утверждаете, что можно говорить о биекции, не говоря о множествах?

Биекция - это всего лишь взаимно однозначное отображение. Между чем и чем - это уж можете говорить как нравится. Традиционно, да, принято говорить, что между множествами. Но можно выразиться и на языке чистой логики (исчисления предикатов) - в терминах: "Для любого $y$, обладающего свойством $Y$, существует $x$, обладающий свойством $X$, такой, что...".

[EminentVictorians]

epros в сообщении #1604978 писал(а):

Биекция - это всего лишь взаимно однозначное отображение. Между чем и чем - это уж можете говорить как нравится. Традиционно, да, принято говорить, что между множествами. Но можно выразиться и на языке чистой логики (исчисления предикатов) - в терминах: "Для любого $y$, обладающего свойством $Y$, существует $x$, обладающий свойством $X$, такой, что...".

Да, я именно это и имел в виду. Можно взять какую-нибудь слабую теорию, в которой нету никаких множеств, и явно писать: каждому $a$ с таким-то свойством, соответствует $x$ с таким-то свойством, разным $a$ и $b$ соответствуют разные $x$ и $y$, для любого $z$ найдется $c$... В общем, как-то так. Множеств $A = \{a, b, c...\}$ и $B = \{x, y, z...\}$ у нас нету, и даже биекции, как функции, тоже нету, но биекцию как-бы установили. Здорово, что здесь получился консенсус.

Что такое биекция (в Вашем варианте) - я понял. Дальше идет изоморфизм. Вот Вы говорите, что изоморфизм сохраняет все свойства. Следует ли из этого, что "образ" изоморфизма должен совпадать с его областью определения? ("образ" пишу в кавычках, т.к. в множество он собираться не обязан, но лучшего слова нету)

[mihaild]

epros в сообщении #1604961 писал(а):

А зачем? Пусть не соответствует

Потому что это определение "поле $A$ содержит подполе $B$, изоморфное полю $C$".

epros в сообщении #1604961 писал(а):

"Таких" может быть и много, но само $\mathbb{R}$-то одно. Мы просто скажем про $\mathbb{R}$ в двух местах

Что именно скажем?

epros в сообщении #1604961 писал(а):

Мне эта аналогия не кажется подходящей, поскольку матрицы $n \times n$ и $n$-мерные векторы принадлежат непересекающимся классам

Но матрицы $n \times n$ на вектора-столбцы умножать можно.
Я про то, что, хотя в $n$-мерном векторном пространстве есть базис, встроенных "координат", необходимых для умножения его элементов на матрицы, нет. И аналогично в $\mathbb C$ можно выбрать подполе, изоморфное $\mathbb R$, но нельзя это сделать каноническим образом.

[vicvolf]

В книге Куликова "Алгебра и теория чисел" из определений и утверждений на стр. 157-162 следует.

Пусть имеется поле действительных чисел $F$ с множеством $R$. Тогда $K$ является полем комплексных чисел c множеством $C$, если выполняются условия:

1. $F$ является подполем $K$.

2. Cуществует элемент $i \in C$ такой, что $i^2=-1$.

3. Каждый элемент $z \in C$ представим в виде $z=a+bi$, где $a,b \in R$.

Из условия 3 следует, что при $b=0$ значение $z=a$ является действительным числом.

[KhAl]

Alexey Rodionov
Так что Вы думаете насчёт своего определения $\mathbb{C}$? Всё ещё всё в порядке? Сможете доказать, что если $\mathbb{K} \subset \mathbb{C}$ — подполе, изоморфное $\mathbb{R}$, то $\mathbb{C} = \mathbb{K} + i\mathbb{K}$?

[epros]

EminentVictorians в сообщении #1604981 писал(а):

Вот Вы говорите, что изоморфизм сохраняет все свойства. Следует ли из этого, что "образ" изоморфизма должен совпадать с его областью определения?

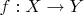
Что, простите? Если Ваша цель заключается в том, чтобы определить изоморфизм без использования слова "множества", то сколько угодно. Сначала говорите, что существует биекция $f:X \to Y$ в указанном выше смысле. Потом пишете что-нибуль вроде: Для любых $x_1, x_2, x_3$, обладающих свойством $X$, $x_1+x_2=x_3 \leftrightarrow f(x_1)+f(x_2)=f(x_3)$. И для других операций аналогично. Только зачем Вам это?

mihaild в сообщении #1604984 писал(а):

Потому что это определение "поле $A$ содержит подполе $B$, изоморфное полю $C$".

И что изменится в этом определении, если вместо "изоморфное полю $C$" будет написано; "биективное $C$"? С учетом того, что нам без разницы соответствуют ли чему-то операции на $C$.

mihaild в сообщении #1604984 писал(а):

Что именно скажем?

1) $\mathbb{C}$ - поле, в котором уравнение $x^2+1=0$ разрешимо, содержащее подполе $\mathbb{R}$.
2) Не существует строгого подполя $\mathbb{C}$, в котором уравнение $x^2+1=0$ разрешимо и которое содержит подполе $\mathbb{R}$.

mihaild в сообщении #1604984 писал(а):

И аналогично в $\mathbb C$ можно выбрать подполе, изоморфное $\mathbb R$, но нельзя это сделать каноническим образом.

Я не понял эту мысль. Возможно, что в $\mathbb{C}$ можно выбрать подполе, изоморфное $\mathbb{R}$ каким-то "неканоническим" образом. Но если аксиоматика говорит нам, что одним из подполей $\mathbb{C}$ является поле, на котором выполняется вся аксиоматика $\mathbb{R}$, то по-моему его можно смело считать за поле $\mathbb{R}$. Далее проблема сводится только к тому, чтобы корректно сформулировать аксиому про "минимальность" $\mathbb{C}$. И, по-моему, формулировка (2) такова, что исключает возможность построения для $\mathbb{R}+i\mathbb{R}$ строгого подполя, которое бы её нарушало, ибо в формулировках (1) и (2) упоминается одно и то же подполе $\mathbb{R}$, а не два разных подполя, изоморфных друг другу в каком-либо смысле.

[mihaild]

epros в сообщении #1605012 писал(а):

Сначала говорите, что существует биекция $f:X \to Y$ в указанном выше смысле. Потом пишете что-нибуль вроде: Для любых $x_1, x_2, x_3$, обладающих свойством $X$, $x_1+x_2=x_3 \leftrightarrow f(x_1)+f(x_2)=f(x_3)$.

Это же будет в итоге элементарная эквивалентность, а не изоморфизм.

epros в сообщении #1605012 писал(а):

И что изменится в этом определении, если вместо "изоморфное полю $C$" будет написано; "биективное $C$"?

То окажется, что в любом хотя бы континуальном поле есть подполе, "изоморфное" $\mathbb R$.

epros в сообщении #1605012 писал(а):

1) $\mathbb{C}$ - поле, в котором уравнение $x^2+1=0$ разрешимо, содержащее подполе $\mathbb{R}$.

А что значит "содержит подполе $\mathbb R$"? "Содержит подполе, в котором при $c \neq 0$ ровно одно из уравнений $x^2 = c$ и $x^2 = -c$ разрешимо; элементы, для которых оно разрешимо, называются положительными, и выполнены все какие положены свойства порядка, включая полноту"? Тогда второе требование невыполнимо.

epros в сообщении #1605012 писал(а):

Но если аксиоматика говорит нам, что одним из подполей $\mathbb{C}$ является поле, на котором выполняется вся аксиоматика $\mathbb{R}$

Если Вы в аксиоматику $\mathbb R$ включаете порядок сам по себе, то непонятно, что вообще значит "на подполе выполняется эта аксиоматика". Если Вы выражаете порядок через арифметику, то подполей, на которых выполнены все нужные свойства порядка при таком введении, куча.

Мне всё же нравится аналогия с векторными пространствами. Например пространство многочленов не выше второй степени над $\mathbb R$ - трехмерное векторное пространство. Но совершенно непонятно, какой оператор на нём задается матрицей $\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{pmatrix}$.

[Alexey Rodionov]

EminentVictorians в сообщении #1604824 писал(а):

Alexey Rodionov в сообщении #1604820 писал(а):

то есть обязательно включить в С числа вида $a+ ib$ .

Alexey Rodionov, Что такое "$+$" в этой цитате?

В поле $ C $ есть числа $a,b$ из поля изоморфного $R$. Есть и мнимая единица $i$. Стало быть, там же их суммы и произведения. И, похоже, больше там ничего не нужно. И выбросить ничего нельзя.

-- 13.08.2023, 02:12 --

epros в сообщении #1604861 писал(а):

Ничто не мешает на этом поле определить норму.
А попробуйте.

А вот $(a^2+ b^2) ^ \frac{1}{2}$.

-- 13.08.2023, 02:23 --

[mihaild]

Alexey Rodionov в сообщении #1605028 писал(а):

В поле $ C $ есть числа $a,b$ из поля изоморфного $R$.

Из которого?

Alexey Rodionov в сообщении #1605028 писал(а):

Не так давно я этот вопрос поднимал и в личку получил замечательный ответ: почему бы не умножить, если они умножаются

Так а что провокативного-то?
И нет, не умножаются. Умножаются только если зафиксировать базис.