Для.

все по-прежнему работает.
Никакого док-ва нет. Имеющееся "доказательство" сводится к следующему:
1. Получен некий многочлен

, который имеет три корня при

:

.
2. Далее утверждается, что имеются три корня

, для которых значение имеется некоторое отрицательное значение

и три корня

, для которых значение имеется некоторое положительное значение

.
При этом за всё время обсуждения темы, само ур-ние, из которого получаются эти корни, не дается. Предлагается самим догадаться, что это за ур-ние.
3. Обнаруживается, что эти корни связаны соотношением

4. Далее делается предположение, что все корни - рациональные.
Это уже само по себе странное предположение, потому что на этом этапе целые числа

могут быть любыми. Заявление, что они вообще говоря не любые, будет сделано в конце "док-ва" и то не на рациональности/иррациональности, а из условия, что
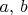
взаимно просты. Поэтому для п. 4 "целые числа

могут быть любыми" - верно.
Что кубическое ур-ние с целыми коэффициентами в общем случае ,не может иметь три рациональных корня, факт очевидный и проверяется на массе примеров.
Казалось бы разумным исследовать форму этих корней и выяснить, когда все три могут быть рациональными. Но Вы идете своим путем.
5. Предположение, что все корни - рациональные, доказывается следующим образом:
Вводится замена переменной

и

.
Очевидно, что при такой замене набор корней переходит

и наоборот. Знак у многочлена меняется, корни, дающие его положительное значение, меняются на корни, дающие отрицательное значение.
Затем делается еще одна замена переменной

. Корни нового многочлена не находятся, но делаются различные предположения о некоей связи между новым набором корней

и точкой

.
Но при линейном сдвиге аргумента весь набор корней

сдвинется как целое на

. Ничего более не произойдет.
Если корни

были иррациональными, то и остальные корни, полученные из них сдвигом на рациональное число, также останутся иррациональными.
Ничего больше в представленном док-ве нет. Если Вы с этим не согласны, почему бы тогда просто не выполнить все преобразования аргумента в исходном многочлене и показать "связь между корнями и точкой

" в явном виде?