Onoochin,
Antoshka 3.1.1 поскольку
функция

является целой рациональной функцией, непрерывна и определена при всех значениях

и ее значение равно нулю в точках 0, h и с,
существует либо две точки , в которых она принимает одинаковые отрицательные значения ,

и

, (или только одна, если

-критическая точка), либо, две точки в которых она принимает одинаковые положительные значения ,

и

( (или только одна, если

-критическая точка).
Эти числа действительные (поскольку если они они комплексные, Это противоречит существованию рационального

между

и

Но если существуют две такие точки, и

, то

,
что невозможно,
Как Вы можете писать такое?
У Вас многочлен

. При некотором

его значение

. Уравнение

имеет число корней, равных

. У Вас вместо

должно быть

, где часть корней - комплексные числа. Что Вы с ними делать будете?
Если уж Вы хотите продемонстрировать док-во для третьей степени, распишите всё подробно с преобразованиями для многочленов вместо графиков.
Уже всё разобрали и исправили. Посмотрите, пожалуйста, более позднее сообщение.
Доказательство для третьей степени отличается от доказательство для более высоких степеней.
Для более высоких степеней всё гораздо проще:
Ферма утверждал, что уравнение

не имеет решений в рациональных числах.
Попробуем доказать обратное.
Предположим, что такое решение существует
при

,

,

,
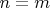
, где

,

,

- целые положительные взаимно простые числа и

, то есть

.

-Нечётное положительное число,

1.1.

, где

- целое положительное число

, где

- целое положительное число.
1.2.

,

Перемножаем левые и правые части, получаем:

,

1.3.

,

(п.1.1). Перемножаем левые и правые части, получаем:

, следовательно,

.
2.1.1 функция

в точках

и

принимает одинаковые значения разных знаков и она является целой рациональной функцией, непрерывна и определена при всех значениях

, следовательно, между

и

существует точка ( назовем ее

, значение функции в которой равно

.
2.1.3 Найдем все точки, значение функции в которых равно нулю.

.

или


,

отсюда

или

.
Поскольку

,

,

-рациональное число,
3.1.1.Найдём критические точки функции



если

или



3.1.1 поскольку
функция

является целой рациональной функцией, непрерывна и определена при всех значениях

и ее значение равно нулю в точках 0, h и с,
существует либо две точки , в которых она принимает одинаковые отрицательные значения ,если

,

и

, (или только одна, если

-критическая точка), либо, две точки в которых она принимает одинаковые положительные значения , если

,

и

( (или только одна, если

-критическая точка), .
Эти числа действительные (поскольку если они они комплексные, Это противоречит существованию рационального

между

и

.
Поскольку мы рассматриваем уравнения с нечётной степенью, действительных корней должно быть нечётное число. Это возможно, только если

- критическая точка,

-критическая точка.


.
Поскольку

,

,

- взаимно простые числа, равенства будут выполняться только в том случае,
если

-целое число.

, что возможно только если

-целое число
Пусть

, тогда

,

,

- целое число,

-целое число,

-целое число, что невозможно, поскольку

-целое число.
(если

-целое число,


,

-целое число,

имеет общий делитель с

, что невозможно (

и

-взаимно простые числа)).