Итак, получена система
Получается система
![$\eqno[7]$ $\eqno[7]$](https://dxdy-04.korotkov.co.uk/f/7/a/2/7a243747661defa7fa853ff21ebab51f82.png)
вида
![$$\left\{
\begin{array}{lcl}
F^7(T+1)=2ed,e,d\in\mathbb{R},e>0,d>0\\
(a-FD)T \sqrt[3]{7a}(FD-(a-FD)T)=e^2-d^2\\
(a-FD)^2T^2 \sqrt[3]{7a}+F^7(T+1)=e^2+d^2
\end{array}
\right.$$ $$\left\{
\begin{array}{lcl}
F^7(T+1)=2ed,e,d\in\mathbb{R},e>0,d>0\\
(a-FD)T \sqrt[3]{7a}(FD-(a-FD)T)=e^2-d^2\\
(a-FD)^2T^2 \sqrt[3]{7a}+F^7(T+1)=e^2+d^2
\end{array}
\right.$$](https://dxdy-01.korotkov.co.uk/f/c/7/e/c7e5e3f20c6eaec92459a6e5d5f307b982.png)
 , одно из которых квадратное, а второе кубическое. Как получить такие уравнения?
, одно из которых квадратное, а второе кубическое. Как получить такие уравнения?В получившейся системе
![$\eqno[7]$ $\eqno[7]$](https://dxdy-04.korotkov.co.uk/f/7/a/2/7a243747661defa7fa853ff21ebab51f82.png)
вычтем из третьего уравнения первое. Это даст возможность найти разность чисел

. Затем зная разность чисел, находим сумму чисел из второго уравнения. Получается, что
![$\left\{
\begin{array}{lcl}
e-d=(a-FD)T \sqrt[6]{7a},\\
e+d=FD\sqrt[6]{7a}-(a-FD)T\sqrt[6]{7a}\\
\end{array}
\right.\Rightarrow \left\{
\begin{array}{lcl}
e=FD\sqrt[6]{7a}/2, \\
d=\frac{FD\sqrt[6]{7a}}{2}-(a-FD)T\sqrt[6]{7a}\ \ \ \eqno[8]\
\end{array}
\right.$ $\left\{
\begin{array}{lcl}
e-d=(a-FD)T \sqrt[6]{7a},\\
e+d=FD\sqrt[6]{7a}-(a-FD)T\sqrt[6]{7a}\\
\end{array}
\right.\Rightarrow \left\{
\begin{array}{lcl}
e=FD\sqrt[6]{7a}/2, \\
d=\frac{FD\sqrt[6]{7a}}{2}-(a-FD)T\sqrt[6]{7a}\ \ \ \eqno[8]\
\end{array}
\right.$](https://dxdy-03.korotkov.co.uk/f/2/1/8/2183c2c52fa860211776099266d255bb82.png)
Надо упростить систему
![$\eqno[8]$ $\eqno[8]$](https://dxdy-02.korotkov.co.uk/f/5/4/c/54ca5d3bed8a771e4f908076afc0c3b882.png)
. Делается это, используя соотношения
![$\eqno[4]$ $\eqno[4]$](https://dxdy-03.korotkov.co.uk/f/e/b/1/eb13c3337433f4b11c87f77dbef64b2582.png)
для

, записанные через

, помня при этом, что
 по лемме 2!
по лемме 2! и что

!
Получим
![$$2F=2mw=2(a-b)D^{-1}\Rightarrow \left\{
\begin{array}{lcl}
\cos\gamma=\frac{h_1}{h_2},(h_1,h_2)=1\\
h_1=\frac{FDD\sqrt[3]{7a}}{2}-F^6 \ \eqno[4]\\
h_2=bD\sqrt[3]{7a}+F^6
\end{array}
\right.$$ $$2F=2mw=2(a-b)D^{-1}\Rightarrow \left\{
\begin{array}{lcl}
\cos\gamma=\frac{h_1}{h_2},(h_1,h_2)=1\\
h_1=\frac{FDD\sqrt[3]{7a}}{2}-F^6 \ \eqno[4]\\
h_2=bD\sqrt[3]{7a}+F^6
\end{array}
\right.$$](https://dxdy-03.korotkov.co.uk/f/2/c/3/2c379b19f15b909db30c53faa1ea7a6b82.png)
Получается, что
![$d=\frac{FD\sqrt[6]{7a}}{2}-(a-FD)T\sqrt[6]{7a}=\frac{FD\sqrt[6]{7a}}{2}-\frac{(a-FD)h_1\sqrt[6]{7a}}{h_2}=$ $d=\frac{FD\sqrt[6]{7a}}{2}-(a-FD)T\sqrt[6]{7a}=\frac{FD\sqrt[6]{7a}}{2}-\frac{(a-FD)h_1\sqrt[6]{7a}}{h_2}=$](https://dxdy-01.korotkov.co.uk/f/0/7/6/0766cc4f301b6d9f1baf6e92e78d294782.png)
![$\frac{\frac{FD\sqrt[6]{7a}}{2}h_2-(a-FD)h_1\sqrt[6]{7a}}{h_2}=\frac{\sqrt[6]{7a}F^6(2a-FD)}{2h_2};$ $\frac{\frac{FD\sqrt[6]{7a}}{2}h_2-(a-FD)h_1\sqrt[6]{7a}}{h_2}=\frac{\sqrt[6]{7a}F^6(2a-FD)}{2h_2};$](https://dxdy-02.korotkov.co.uk/f/9/d/f/9dff6f352948e03e17a59dbcfbe3b96982.png)
Вот доказательство того, что

я записал правильно!
ссылкаПоэтому
![$$\left\{
\begin{array}{lcl}
e=DF\sqrt[6]{7a}/2,\\
d=\frac{\sqrt[6]{7a}F^6(2a-FD)}{2h_2}\ \ \ \ \eqno[8.1]\\
\end{array}
\right.$$ $$\left\{
\begin{array}{lcl}
e=DF\sqrt[6]{7a}/2,\\
d=\frac{\sqrt[6]{7a}F^6(2a-FD)}{2h_2}\ \ \ \ \eqno[8.1]\\
\end{array}
\right.$$](https://dxdy-02.korotkov.co.uk/f/d/e/8/de821976bc40f7725e5f1ef6fbabadb682.png)
Надо выразить две величины из системы
![$\eqno[7]$ $\eqno[7]$](https://dxdy-04.korotkov.co.uk/f/7/a/2/7a243747661defa7fa853ff21ebab51f82.png)
, а именно

и

в терминах

, чтобы получить квадратное и кубическое уравнение относительно

! Сначала из соотношения для

выражаем

, то есть
![$e=\frac{FD\sqrt[6]{7a}}{2}\Rightarrow D=\frac{2e}{F\sqrt[6]{7a}}\Rightarrow D^7=\frac{(2e)^7}{F^7\sqrt[6]{7a}\cdot 7a}\Rightarrow \frac{D^7}{F^7}=\frac{(2e)^7}{F^{14}7a\sqrt[6]{7a}};$ $e=\frac{FD\sqrt[6]{7a}}{2}\Rightarrow D=\frac{2e}{F\sqrt[6]{7a}}\Rightarrow D^7=\frac{(2e)^7}{F^7\sqrt[6]{7a}\cdot 7a}\Rightarrow \frac{D^7}{F^7}=\frac{(2e)^7}{F^{14}7a\sqrt[6]{7a}};$](https://dxdy-03.korotkov.co.uk/f/6/5/4/654647afcdad6fc138d6cd51a000bc2582.png)
Сейчас из соотношения для

выражаем

, то есть
![$a\sqrt[6]{7a}=\frac{e-d+2eT}{T};$ $a\sqrt[6]{7a}=\frac{e-d+2eT}{T};$](https://dxdy-02.korotkov.co.uk/f/9/e/1/9e192a44966363eabf66aae0ee50193982.png)
Выражаем из первого уравнения системы
![$\eqno[7]$ $\eqno[7]$](https://dxdy-04.korotkov.co.uk/f/7/a/2/7a243747661defa7fa853ff21ebab51f82.png)

, то есть
![$F^7(T+1)=2ed\Rightarrow F^7=\frac{2ed}{T+1}\Rightarrow F^{14}=\frac{4e^2d^2}{(T+1)^2};a\sqrt[6]{7a}\cdot F^7=\frac{e-d+2eT}{T}\cdot\frac{2ed}{T+1};$ $F^7(T+1)=2ed\Rightarrow F^7=\frac{2ed}{T+1}\Rightarrow F^{14}=\frac{4e^2d^2}{(T+1)^2};a\sqrt[6]{7a}\cdot F^7=\frac{e-d+2eT}{T}\cdot\frac{2ed}{T+1};$](https://dxdy-03.korotkov.co.uk/f/e/5/7/e57666abf1057ade1170eb35f0b4564282.png)
Теперь есть все необходимое, чтобы записать

! Смотрите, сначала подставляем последнее полученное уравнение в знаменатель дроби
![$D^7=\frac{(2e)^7}{F^7(7a\sqrt[6]{7a})};$ $D^7=\frac{(2e)^7}{F^7(7a\sqrt[6]{7a})};$](https://dxdy-04.korotkov.co.uk/f/7/c/4/7c4cf5290465c7d9f21e69286864e30a82.png)
Затем находим
![$F^{14}\cdot 7a\sqrt[6]{7a}$ $F^{14}\cdot 7a\sqrt[6]{7a}$](https://dxdy-04.korotkov.co.uk/f/f/4/d/f4df97eea73aa72308321ba93ed5af2982.png)
с помощью вышеполученных уравнений для

и для
![$a\sqrt[6]{7a};$ $a\sqrt[6]{7a};$](https://dxdy-01.korotkov.co.uk/f/c/b/5/cb51215dc5455aa334c41c81ef91a06382.png)
Получится, что
![$F^{14}7a\sqrt[6]{7a}=\frac{4e^2d^2}{(T+1)^2}\cdot\frac{7(e-d+2eT)}{T}$ $F^{14}7a\sqrt[6]{7a}=\frac{4e^2d^2}{(T+1)^2}\cdot\frac{7(e-d+2eT)}{T}$](https://dxdy-01.korotkov.co.uk/f/0/4/b/04b5240ee61311fe00fdece68690df8582.png)
, что даёт возможность найти
![$\frac{D^7}{F^7}=\frac{(2e)^7}{F^{14}\sqrt[6]{7a}7a}$ $\frac{D^7}{F^7}=\frac{(2e)^7}{F^{14}\sqrt[6]{7a}7a}$](https://dxdy-02.korotkov.co.uk/f/1/3/a/13a5a16cad64e43cd2509c10979119ba82.png)
!
Получается система
![$\left\{
\begin{array}{lcl}
\frac{D^7}{F^7}=\frac{32e^5(T+1)^2T}{7d^2(e-d+2eT)}, \\ D^7=\frac{64e^6(T+1)T}{7d(e(2T+1)-d)} \ \eqno[9]
\end{array}
\right.$ $\left\{
\begin{array}{lcl}
\frac{D^7}{F^7}=\frac{32e^5(T+1)^2T}{7d^2(e-d+2eT)}, \\ D^7=\frac{64e^6(T+1)T}{7d(e(2T+1)-d)} \ \eqno[9]
\end{array}
\right.$](https://dxdy-03.korotkov.co.uk/f/a/7/c/a7c8dbcc098097ef81488fc93ca8965f82.png)
Дальше уже просто. Переписываем каждое из уравнений системы
![$\eqno[9]$ $\eqno[9]$](https://dxdy-04.korotkov.co.uk/f/f/0/6/f066c6c7279c142bed8c917db7da8fd782.png)
в виде алгебраических уравнений относительно

в третьей и второй степени, приводя все к общему знаменателю и максимально упрощая, используя уже упрощенные соотношения
![$\eqno[8.1]$ $\eqno[8.1]$](https://dxdy-02.korotkov.co.uk/f/5/c/c/5cc7337238053dda41a07848858aa8a182.png)
![$\left\{
\begin{array}{lcl}
e=DF\sqrt[6]{7a}/2,\\
d=\frac{\sqrt[6]{7a}F^6(2a-FD)}{2h_2}\\
\end{array}
\right.$ $\left\{
\begin{array}{lcl}
e=DF\sqrt[6]{7a}/2,\\
d=\frac{\sqrt[6]{7a}F^6(2a-FD)}{2h_2}\\
\end{array}
\right.$](https://dxdy-02.korotkov.co.uk/f/1/c/0/1c0453096f0d056f53647fc9511b167e82.png)
Сначала я покажу, как выглядят уравнения системы
![$\eqno [9]$ $\eqno [9]$](https://dxdy-01.korotkov.co.uk/f/8/6/6/866ec796984332b94ac905cbee42380782.png)
в терминах

, затем я их запишу с помощью соотношений
![$\eqno[8.1]$ $\eqno[8.1]$](https://dxdy-02.korotkov.co.uk/f/5/c/c/5cc7337238053dda41a07848858aa8a182.png)
! Итак
![$$\left\{
\begin{array}{lcl}
32e^5F^7T^3+64e^5F^7T^2+(32e^5F^7-14ed^2D^7)T-7d^2D^7(e-d)=0\\
64e^6T^2+2e(32e^5-7dD^7)T-7dD^7(e-d)=0\ \ \ \ \ \eqno[10]
\end{array}
\right.$$ $$\left\{
\begin{array}{lcl}
32e^5F^7T^3+64e^5F^7T^2+(32e^5F^7-14ed^2D^7)T-7d^2D^7(e-d)=0\\
64e^6T^2+2e(32e^5-7dD^7)T-7dD^7(e-d)=0\ \ \ \ \ \eqno[10]
\end{array}
\right.$$](https://dxdy-01.korotkov.co.uk/f/0/8/3/083a18d5fc714419753c0a3e9b97c2a582.png)
Вот доказательство того, что каждое из уравнений системы
![$\eqno[10]$ $\eqno[10]$](https://dxdy-04.korotkov.co.uk/f/b/f/c/bfcb08796dc4e1cde52e92357d9e516582.png)
записано правильно через
 ссылка на первое уравнениессылка на второе уравнение
ссылка на первое уравнениессылка на второе уравнениеЗачем я записал два уравнения в системе
![$\eqno[10]$ $\eqno[10]$](https://dxdy-04.korotkov.co.uk/f/b/f/c/bfcb08796dc4e1cde52e92357d9e516582.png)
? Для того, чтобы найти все три корня кубического уравнения относительно

, а затем с помощью квадратного уравнения понять, какой из этих трех корней нам нужен! Значит берём в системе
![$\eqno[10]$ $\eqno[10]$](https://dxdy-04.korotkov.co.uk/f/b/f/c/bfcb08796dc4e1cde52e92357d9e516582.png)
соответствующий кубический и квадратный многочлен, делим их уголком друг на друга, а затем находим корень

как корень линейного уравнения в силу того, что степень остатка от деления многочленов должна быть хотя бы на единицу меньше, чем степень делителя!
В wolfram mathematica это записывается в виде командКод:
Eq1=... (кубическое уравнение)
Eq2=... (квадратное уравнение)
Ost=PolynomialRemainder[Eq1,Eq2,T]//Factor
Solve[Ost==0,T]//Factor
Получится, что корень имеет вид
![$T=\frac{-(e-d)(64e^6d-32e^5F^7-7dF^7D^7)}{2e(64e^6d-16e^5F^7+16e^4dF^7-7dF^7D^7)};\eqno[11]$ $T=\frac{-(e-d)(64e^6d-32e^5F^7-7dF^7D^7)}{2e(64e^6d-16e^5F^7+16e^4dF^7-7dF^7D^7)};\eqno[11]$](https://dxdy-04.korotkov.co.uk/f/f/d/1/fd14dec50a884ee4994dce417636ac7282.png) Могут ли числитель и знаменатель дроби
Могут ли числитель и знаменатель дроби ![$\eqno[11]$ $\eqno[11]$](https://dxdy-03.korotkov.co.uk/f/2/b/3/2b3505a9224942b12316a0e9bfdf7b8182.png) быть равными нулю одновременно?
быть равными нулю одновременно? Если нет, это значит, что остаток от деления вышеупомянутых многочленов не равен нулю!
Возьмём числитель дроби
![$\eqno[11]$ $\eqno[11]$](https://dxdy-03.korotkov.co.uk/f/2/b/3/2b3505a9224942b12316a0e9bfdf7b8182.png)
, приравнивая каждый сомножитель нулю!
Пусть 
попробуем приравнять сомножители в знаменателе нулю, начиная с левого!

Обратимся к соотношениям
![$\eqno[8.1]$ $\eqno[8.1]$](https://dxdy-02.korotkov.co.uk/f/5/c/c/5cc7337238053dda41a07848858aa8a182.png)
и получим
![$e=DF\sqrt[6]{7a}/2\Rightarrow Da=0\Rightarrow a=0$ $e=DF\sqrt[6]{7a}/2\Rightarrow Da=0\Rightarrow a=0$](https://dxdy-03.korotkov.co.uk/f/e/a/2/ea2f0558a445e40b5baca5109b9670a482.png)
, потому что

в любом случае нечетное! Но
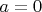
влечет

по лемме 2, значит

по лемме 1!
Противоречие!Приравняв нулю второй сомножитель в знаменателе дроби
![$\eqno[11]$ $\eqno[11]$](https://dxdy-03.korotkov.co.uk/f/2/b/3/2b3505a9224942b12316a0e9bfdf7b8182.png)
получится, учитывая, что

Обратимся к соотношениям
![$\eqno[8.1]$ $\eqno[8.1]$](https://dxdy-02.korotkov.co.uk/f/5/c/c/5cc7337238053dda41a07848858aa8a182.png)
и получим
![$e=DF\sqrt[6]{7a}/2\Rightarrow aFD=0$ $e=DF\sqrt[6]{7a}/2\Rightarrow aFD=0$](https://dxdy-04.korotkov.co.uk/f/b/1/8/b18584146e96e65eb8796414e809068682.png)
, потому что

попарно взаимно простые по лемме 2! Но

вообще нечетные по лемме 1, про
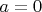
уже говорилось выше! Значит случай

невозможен!
Пусть теперь второй сомножитель в числителе равен нулю! То есть

тогда если в знаменателе

, то получаем противоречие! Значит равен нулю второй сомножитель знаменателя, то есть

значит получаем систему

Вычитаем одно уравнение из другого и получаем

!
Опять противоречие, так как

, а

нечетное по лемме 1!
Значит нужный корень  можно действительно представить в виде дроби
можно действительно представить в виде дроби ![$\eqno[11]$ $\eqno[11]$](https://dxdy-03.korotkov.co.uk/f/2/b/3/2b3505a9224942b12316a0e9bfdf7b8182.png) !
!Вот настала пора решить кубическое уравнение из системы
![$\eqno[10]$ $\eqno[10]$](https://dxdy-04.korotkov.co.uk/f/b/f/c/bfcb08796dc4e1cde52e92357d9e516582.png)
!
Оно будет иметь три корня! Дробь
![$\eqno[11]$ $\eqno[11]$](https://dxdy-03.korotkov.co.uk/f/2/b/3/2b3505a9224942b12316a0e9bfdf7b8182.png)
поможет узнать, какой из трех корней нам нужен, ведь если ее подставить в кубическое уравнение системы
![$\eqno[10]$ $\eqno[10]$](https://dxdy-04.korotkov.co.uk/f/b/f/c/bfcb08796dc4e1cde52e92357d9e516582.png)
, то получится нуль тождественный, то есть получается, что какой-то из корней представляется двумя способами!
В wolfram mathematica для этого надо набрать командуКод:
T=...(дробь [11])
ExpandAll[Eq1]//Fullsimplify
Если все набрано правильно, должен получиться тождественный нуль!
Короче, решаем кубическое уравнение из системы
![$\eqno[10]$ $\eqno[10]$](https://dxdy-04.korotkov.co.uk/f/b/f/c/bfcb08796dc4e1cde52e92357d9e516582.png)
вида
![$32e^5F^7T^3+64e^5F^7T^2+(32e^5F^7-14ed^2D^7)T-7d^2D^7(e-d)=0;\eqno[10.1]$ $32e^5F^7T^3+64e^5F^7T^2+(32e^5F^7-14ed^2D^7)T-7d^2D^7(e-d)=0;\eqno[10.1]$](https://dxdy-01.korotkov.co.uk/f/4/2/a/42a3f8b0bc113dc1a88d6f9f477a9d3582.png)
Вот ссылка на решение
ссылка Как видите, у него даже в самом компактном варианте длинные корни получаются! По ссылке видно, что два корня сопряженные, поэтому давайте возьмём корень, который не сопряжен, может это он записывается в виде дроби
![$\eqno[11]$ $\eqno[11]$](https://dxdy-03.korotkov.co.uk/f/2/b/3/2b3505a9224942b12316a0e9bfdf7b8182.png)
?
Чтобы это узнать, сделаем следующее. Предположим это реально он.
Сначала переносим

налево и записываем корень в общем виде, чтобы наглядно было
![$T+2/3=h_3\sqrt[3]{h_4}+\frac{h_5}{\sqrt[3]{h_4}};$ $T+2/3=h_3\sqrt[3]{h_4}+\frac{h_5}{\sqrt[3]{h_4}};$](https://dxdy-01.korotkov.co.uk/f/4/f/5/4f5d59faa258c04f15e1b624368d838182.png)
Возводим обе части полученного равенства в куб следующим образом.
Обозначим корень, который записывается через дробь
![$\eqno[11]$ $\eqno[11]$](https://dxdy-03.korotkov.co.uk/f/2/b/3/2b3505a9224942b12316a0e9bfdf7b8182.png)
как

тогда
![$(T_f+2/3)^3=(h_3\sqrt[3]{h_4}+\frac{h_5}{\sqrt[3]{h_4}})^3\Leftrightarrow (T_f+2/3)^3=(h_3\sqrt[3]{h_4})^3+(\frac{h_5}{\sqrt[3]{h_4}})^3+$ $(T_f+2/3)^3=(h_3\sqrt[3]{h_4}+\frac{h_5}{\sqrt[3]{h_4}})^3\Leftrightarrow (T_f+2/3)^3=(h_3\sqrt[3]{h_4})^3+(\frac{h_5}{\sqrt[3]{h_4}})^3+$](https://dxdy-01.korotkov.co.uk/f/0/6/8/068d0a5b7887a8af0726baa953b8b63582.png)
![$3\frac{h_5}{\sqrt[3]{h_4}}\cdot h_3\sqrt[3]{h_4}(T_f+2/3);\eqno[12]$ $3\frac{h_5}{\sqrt[3]{h_4}}\cdot h_3\sqrt[3]{h_4}(T_f+2/3);\eqno[12]$](https://dxdy-03.korotkov.co.uk/f/a/f/f/affc2ae3d6b50c00bca6b45916f2710c82.png)
Если в уравнении
![$\eqno[12]$ $\eqno[12]$](https://dxdy-02.korotkov.co.uk/f/d/e/4/de4dc6bd7c11ad961c1cb8419688674182.png)
раскрыть скобки и упростить все, то получится тождественный нуль! Чтобы в этом убедиться, набираем команду
Код:
Tf=...(дробь[11])
h_3=...
h_4=...
h_5=...
ExpandAll[(Tf+2/3)^3-h3^3h4-h5^3/h4-3h5 h3(Tf+2/3)]//Fullsimplify
Это значит, что нужный корень найден, потому что если взять сопряженные корни и с ними проделать ту же процедуру, то тождественный нуль не получается! Ну а раз нужный корень найден, остаётся записать кубическое уравнение ![$\eqno[10.1]$ $\eqno[10.1]$](https://dxdy-01.korotkov.co.uk/f/0/d/1/0d10cefb0b07148a1f126aeb0dd10d1182.png) через соотношения
через соотношения ![$\eqno[8.1]$ $\eqno[8.1]$](https://dxdy-02.korotkov.co.uk/f/5/c/c/5cc7337238053dda41a07848858aa8a182.png) , решив его в wolfram mathematica. Для этого набираем команды
, решив его в wolfram mathematica. Для этого набираем командыКод:
e=...
d=....
Eq3=Factor[Eq1(кубическое уравнение [10.1])]
Вот как выглядит кубическое уравнение в результате выполнения команды
Лемма 3Уравнение
![$\eqno[10.1]$ $\eqno[10.1]$](https://dxdy-01.korotkov.co.uk/f/0/d/1/0d10cefb0b07148a1f126aeb0dd10d1182.png)
после подстановки в него соотношений
![$\eqno[8.1]$ $\eqno[8.1]$](https://dxdy-02.korotkov.co.uk/f/5/c/c/5cc7337238053dda41a07848858aa8a182.png)
и упрощения принимает вид такой
![$8h_2^3\sqrt[3]{7a}T^3+16h_2^3\sqrt[3]{7a}T^2+(8h_2^3-14F(2a-FD)^2h_2D^3)T+$ $8h_2^3\sqrt[3]{7a}T^3+16h_2^3\sqrt[3]{7a}T^2+(8h_2^3-14F(2a-FD)^2h_2D^3)T+$](https://dxdy-03.korotkov.co.uk/f/6/5/8/658d93a16aab679fe110a51e9829201e82.png)
![$7F(2a-FD)^2D^2(F^5(2a-FD)-h_2D)=0;\eqno[10.2]$ $7F(2a-FD)^2D^2(F^5(2a-FD)-h_2D)=0;\eqno[10.2]$](https://dxdy-02.korotkov.co.uk/f/5/b/3/5b35207a1593554072e8a26b5beb31b782.png) И вот как выглядят его корни
И вот как выглядят его корниЗначит набираем команду и получаем корни, предварительно заменив
![$(2a-FD)\to d_1,\frac{\sqrt[6]{7a}}{2}\to c_1$ $(2a-FD)\to d_1,\frac{\sqrt[6]{7a}}{2}\to c_1$](https://dxdy-02.korotkov.co.uk/f/9/8/7/9876efe4542113c0a40c1abe307c91af82.png)
, чтобы корни были максимально компактными. Затем в уже полученных корнях делаем обратную подстановку.
Код:
Eq4=...(уравнение [10.2])
Solve[Eq4==0,T]//Fullsimplify

, где
![$\left\{
\begin{array}{lcl}
j_1=\frac{r_1}{r_2\sqrt[3]{r_3}}\\
j_2=\frac{\sqrt[3]{r_3}}{r_2} \ \ \eqno[11]\\
\end{array}
\right. $ $\left\{
\begin{array}{lcl}
j_1=\frac{r_1}{r_2\sqrt[3]{r_3}}\\
j_2=\frac{\sqrt[3]{r_3}}{r_2} \ \ \eqno[11]\\
\end{array}
\right. $](https://dxdy-02.korotkov.co.uk/f/9/5/9/9590cddc18dbc5392857991281a1e8d882.png)
![$\left\{
\begin{array}{lcl}
r_1=4\sqrt[6]{7a}^2h_2^2+21(2a-FD)^2FD^3,\\
r_2=6\sqrt[6]{7a}h_2,\\
r_3=r_4+r_{50}\sqrt{r_{60}}
\end{array}
\right. $ $\left\{
\begin{array}{lcl}
r_1=4\sqrt[6]{7a}^2h_2^2+21(2a-FD)^2FD^3,\\
r_2=6\sqrt[6]{7a}h_2,\\
r_3=r_4+r_{50}\sqrt{r_{60}}
\end{array}
\right. $](https://dxdy-01.korotkov.co.uk/f/4/a/7/4a77ea5b0a1815c160164fc39247e46282.png)
Кроме того,
![$$\left\{
\begin{array}{lcl} r_4=8\sqrt[6]{7a}^3h_2^3-63\sqrt[6]{7a}(2a-FD)^2FD^2(3(2a-FD)F^5+h_2D)/2,\\
r_{50}=3(2a-FD)D,\\
r_{61}=-21F(49(2a-FD)^4F^2D^7+8\sqrt[6]{7a}^4h_2^3((2a-FD)F^5+h_2D))\\
r_{62}=21F(7\frac{\sqrt[6]{7a}^2}{4}(2a-FD)^2FD^2(27(2a-FD)^2F^{10}+18(2a-FD)F^5h_2D-13h_2^2D^2))\\
r_{60}=r_{61}-r_{62}\\
\end{array}
\right.$$ $$\left\{
\begin{array}{lcl} r_4=8\sqrt[6]{7a}^3h_2^3-63\sqrt[6]{7a}(2a-FD)^2FD^2(3(2a-FD)F^5+h_2D)/2,\\
r_{50}=3(2a-FD)D,\\
r_{61}=-21F(49(2a-FD)^4F^2D^7+8\sqrt[6]{7a}^4h_2^3((2a-FD)F^5+h_2D))\\
r_{62}=21F(7\frac{\sqrt[6]{7a}^2}{4}(2a-FD)^2FD^2(27(2a-FD)^2F^{10}+18(2a-FD)F^5h_2D-13h_2^2D^2))\\
r_{60}=r_{61}-r_{62}\\
\end{array}
\right.$$](https://dxdy-03.korotkov.co.uk/f/e/e/e/eee73cfbf216c0f456292ccfe9106d0082.png)
Тут я сразу отмечу, что

, потому что число

делится ровно на два в первой степени, что следует из соотношений
![$\eqno[4]$ $\eqno[4]$](https://dxdy-03.korotkov.co.uk/f/e/b/1/eb13c3337433f4b11c87f77dbef64b2582.png)
Получим
![$$2F=2mw=2(a-b)D^{-1}\Rightarrow \left\{
\begin{array}{lcl}
\cos\gamma=\frac{h_1}{h_2},(h_1,h_2)=1\\
h_1=\frac{FDD\sqrt[3]{7a}}{2}-F^6 \ \eqno[4]\\
h_2=bD\sqrt[3]{7a}+F^6
\end{array}
\right.$$ $$2F=2mw=2(a-b)D^{-1}\Rightarrow \left\{
\begin{array}{lcl}
\cos\gamma=\frac{h_1}{h_2},(h_1,h_2)=1\\
h_1=\frac{FDD\sqrt[3]{7a}}{2}-F^6 \ \eqno[4]\\
h_2=bD\sqrt[3]{7a}+F^6
\end{array}
\right.$$](https://dxdy-03.korotkov.co.uk/f/2/c/3/2c379b19f15b909db30c53faa1ea7a6b82.png)
ниже будет доказательство этого факта!
Сопряженные корни выглядят так Доказательство леммы 3
Доказательство леммы 3Итак, почему вышеупомянутое число делится ровно на 2 в первой степени? Вот берём соотношения
![$\eqno[4]$ $\eqno[4]$](https://dxdy-03.korotkov.co.uk/f/e/b/1/eb13c3337433f4b11c87f77dbef64b2582.png)
и подставляем в это число, расписывая его по модулю четыре. Получается, что

в силу
леммы 1,2, значит

, то есть оно реально делится на два ровно, так как

по любому нечетное, ну а раз так, то

, потому что в противном случае это влечёт
![$\sqrt[6]{7a}=0$ $\sqrt[6]{7a}=0$](https://dxdy-04.korotkov.co.uk/f/f/7/7/f77969615b422e803a9764f310d02f6482.png)
, что невозможно!
Лемма 3 доказана! Нужный корень найден! Продолжение в следующем сообщении!