Для начала докажите, что

, где

— некоторый многочлен. Для этого рассмотрите

.
Смотрите, как решал я. В силу задачи 4.12, в) обсуждаемого задачника я могу написать равенство:
Применяя эту формулу к решаемой задаче, получу:

Принимая во внимание нечетность

в этой задаче, а, значит, и целость чисел

, где

(

тоже целое), переписываю последнее равенство в следующем виде:

Рассматриваю правую часть последнего равенства как многочлен от

. Тогда старший коэффициент этого многочлена равен старшему коэффициенту первой скобки правой части последнего равенства, рассматриваемой как многочлен от

, т. е., равен он

. Корни этого уравнения есть квадраты синусов корней уравнения

, т.е., квадраты синусов таких чисел

, при которых

, но

. Выписываю значения таких

сериями:

. Здесь запись этих значений

продолжается, понятно, неограниченно в обе стороны. Здесь

, принадлежащие одной серии, объединены одной нижней фигурной скобкой. Для чего вводится группировка по сериям, я объясню чуть ниже. Выпишу значения квадратов синусов только что записанных значений

, сохраняя группировку по сериям соответствующим образом:

. Выясню, какие же на самом деле различные значения содержатся в выписанном бесконечном множестве квадратов синусов. Для этого, во-первых, замечу, что, если

- какое-либо натуральное число такое, что

(вообще при такой записи значений

получается, что доказательство я провожу для случая положительного

), а

- вообще произвольное целое число, то имеет место равенство:

, а потому и

. Т. е. для выяснения того, что я поставил целью выяснить выше, достаточно ограничиться одной серией. Именно для этого я и ввел объединение в серии. Возьму простейшую из серий:

. В этой серии, если

- опять-таки

, оговоренное выше, выполняется равенство:

, а, значит, и равенство

. Таким образом, перечень попарно различных квадратов синусов из данной серии выглядит следующим образом:

, т. е., количество этих квадратов синусов равно

, что как раз совпадает со степенью начатого мной рассматриваться выше многочлена от

. На этом основании я делаю вывод, что формула, которую требуется доказать в задаче, правильно записывается следующим образом:

, а это вместе с тем еще и означает, высказывания, сделанные мной здесь:
Короче, на мой весьма ограниченный взгляд, формула, подлежащая доказательству, имеет следующий вид:

.
и здесь:
Или, если прям уж совсем нужно взять наименьшее значение

именно таким, то тогда нужно перед произведением,
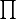
, поставить еще множитель

неверны.
Да-да, конечно, полиномы Лагерра, Чебышева, Эрмита... С этим я уже поверхностно сталкивался. Но сейчас пользоваться этими уже развитыми теориями нельзя. Сейчас нельзя пользоваться даже тем поверхностным, что удалось найти мне тогда.