Вы уж как-нибудь определитесь: полезен этот объект потому, что бесполезен или, наоборот, бесполезен потому, что полезен.
Я в своем посте вполне точно написал: бесполезен неопределенный интеграл. Понятие первообразной и теорему о множестве первообразных на связном промежутке считаю полезной.
Зорич тут абсолютно не при чём, у всех идёт ровно так. По очевидной причине -- это совершенно разные тематики.
По мне странно изучать неопределенный интеграл до определенного, поскольку первый полностью сводится ко второму. Зачем доказывать отдельно теоремы о неопределенном интеграле, если их можно легко вывести из соответствующих теорем об определенном?
План такой:
1)Вводим определенный интеграл и доказываем его основные свойства
2)Доказываем теорему Барроу и Ньютона-Лейбница
3)Во всех задачах, где требуется найти неопределенный интеграл, заменяем значок неопределенного интеграла на интеграл с переменным верхним пределом (а в конце добавляем "+с" если больно уж так надо - я, например, никогда не добавляю).
Теорема Ньютона-Лейбница доказывается действительно по щелчку, но вовсе не из-за Барроу, а из-за теоремы Лагранжа о конечных приращениях (благодаря ней всегда можно выбирать такие интегральные суммы, которые попросту равны полному приращению функции).
Я из Барроу доказывал. Берем непрерывную функцию

. Для нее корректно определен интеграл с переменным верхним пределом

. Имеем:

. Величина
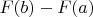
не зависит от выбора конкретной первообразной

, т.к. они все отличаются на константу. Вот и все, теорема Ньютона-Лейбница доказана. Теорема Лагранжа нигде не использовалась.



