Так эта задача уже озвучивалась. Найти минимальную 15-шку. Или, проверив все возможные варианты, доказать, что существующая минимальна.
Это совершенно нереально, по нескольким причинам:
1. Не доказано (или я не помню) что минимальная пятнашка имеет формат КМК. Например проверить что нет решений с

легко за пару минут, а вот проверка отсутствия решений с

(например для чисел 5-13) уже потребует сравнимого с затраченным времени. А ещё в принципе может быть и

и
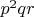
. Да, все эти варианты намного реже КМК, но не доказано что они не дают меньшего решения, вдруг какая аномалия.
2. Компиляция каждого набора паттернов занимает пару часов, даже не считая вычисления по ним, только на компиляцию всех 2700 вариантов замены одного 37 на другие простые (чтобы прокрутить все паттерны за один раз по 227e6 проверок в моей программе) надо
 месяцев!
месяцев! Только на компиляцию! Плюс они ещё сколько-то времени будут считать. Очень сильно вряд ли Вам повезёт прямо с первыми проверенными вариантами замен и ещё до 1e34 (до которой мне считать порядка 2ч в один поток).
И это замена только одного числа. А ведь менять можно и другие числа, в том числе одновременно несколько ...
3. В этом Вы ошибаетесь: "Ну и шаг в паттернах весьма быстро возрастает: на 22%, на 35%, на 61%, на 75%, ...", вот табличка увеличения шага при замене одного любого числа на другое:
Код:
? forprime(p=41,97, print1("\t",p)); print; forprime(x=17,37, print1(x,":"); forprime(p=41,97, printf("\t%0.4f",p/x)); print)
41 43 47 53 59 61 67 71 73 79 83 89 97
17: 2.4118 2.5294 2.7647 3.1176 3.4706 3.5882 3.9412 4.1765 4.2941 4.6471 4.8824 5.2353 5.7059
19: 2.1579 2.2632 2.4737 2.7895 3.1053 3.2105 3.5263 3.7368 3.8421 4.1579 4.3684 4.6842 5.1053
23: 1.7826 1.8696 2.0435 2.3043 2.5652 2.6522 2.9130 3.0870 3.1739 3.4348 3.6087 3.8696 4.2174
29: 1.4138 1.4828 1.6207 1.8276 2.0345 2.1034 2.3103 2.4483 2.5172 2.7241 2.8621 3.0690 3.3448
31: 1.3226 1.3871 1.5161 1.7097 1.9032 1.9677 2.1613 2.2903 2.3548 2.5484 2.6774 2.8710 3.1290
37: 1.1081 1.1622 1.2703 1.4324 1.5946 1.6486 1.8108 1.9189 1.9730 2.1351 2.2432 2.4054 2.6216
Как прекрасно видно, в порядке увеличения шага замены должны идти в порядке (знаменатель что менять, числитель на что, надеюсь не ошибся):

, обратите внимание на предпоследнюю дробь, дальше таких будет только больше, вплоть до замены одновременно всех 6-ти чисел на другие (уже при шаге всего в 64 раза большем).
Я хотел пойти таким путём, перебрать все возможные варианты замен для плавного увеличения шага, правда не для пятнашки, а для 10-ки, там интервал от минимального шага до обнаруженного намного меньше, всего примерно 100 или 1000 (не помню навскидку, искать же точную цифру незачем), но даже и там количество вариантов растёт слишком быстро и без изменения подхода задача неподъёмная. Для пятнашки же у меня получаются оценки в
миллионы лет счёта если не повезёт и в
тысячи лет если крупно повезёт. Хотите — пробуйте. Я пас.
2. Если и искать минимальную цепочку, то начинать где-то с 10-ки с 12 делителями. То есть с минимальной цепочки, по которой есть только оценка, а не точное значение. При этом сразу нужно озаботиться, чтобы метод поиска обеспечивал доказательство минимальности цепочки.
Это я грубо оценивал где-то в
сотни-тысячи лет счёта если не повезёт. Слишком много вариантов. В принципе такую задачу поставить можно, но ... нужна активная поддержка участников, и не только запустить счёт, а и с математикой, у меня слишком часты ошибки в ней.
Про GPU я буду думать когда будет известно что именно будем считать и будет хоть какая-то оценка требуемого времени и она будет в
месяцы. Потому что достичь теоретически возможного ускорения

кратного ускорения нереально, хорошо если получится на где-то порядок меньше, 10-30 раз. А вот в AVX2 я достигал почти пиковой скорости (на похожих задачах), о чём писал и здесь на форуме. Поиск пятнашки занял 2.5 недели в 4 потока (Ваше везение с выбором диапазона не учитываю) и пока оценка требуемого времени счёта меньше месяца нет смысла тратить неделю-три на оптимизацию под GPU (тем более для меня ускорения вообще не будет из-за отсутствия дискретного GPU).
Jon E. Schoenfield интересуется:
Цитата:
Also, if you have time, do you happen to have an upper bound for A292580(15,4)?
Полагаю, это перспективнее, чем искать минимальную пятнашку.
Полагаю да, всего 4 числа и буквально несколько вариантов паттернов (может и один, пока лишь грубо прикинул).
Кстати и
Hugo van der Sanden с OEIS интересовался программами, пока думаю что и как ему ответить.
на "голом" PARI/GP разница должна быть не столь большая, или нет.
На одинаковых версиях PARI разница должна быть почти строго равна отношению количества потоков и частот. Но есть некоторая разница в скорости между gp64 и gp32 на x64 компах (и эта разница
разная для разных алгоритмов, априори не оценишь, у меня какой-то код выполняется в gp32 быстрее, а большинство быстрее в gp64).
Второй работает, первый нет (Illegal instruction).
Процессор 64-битный AMD A8-7410 APU.
AVX2 он, кажется, не поддерживает, да...
Это не смертельно, но не слишком хорошо, AVX2 заметно быстрее (и немного даже чем ненаписанный AVX). При замерах у меня на компе x32 SSE версия примерно втрое медленнее x64 AVX2 (64с против 23с). Плюс почему-то AMD медленнее Intel на этом коде, хотя по тактам на команды настолько больших отличий не видно. Причина непонятна.
Пока Вам следует пользоваться вариантом x32 SSE (тоже выложен в
моём облаке) и запускать под gp64 (если винда x64).
Как будет определена задача объясню подробнее что и как запускать.



