Образцовая программа (на меньшем интервале, лишь 10^35):
T:\gp64 -q VAL1.gp
183800000000000000000000000000000000000 - start
183900000000000000000000000000000000000 - stop
183880930406850062548257966254326127641: 48, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 24, 48, 24, len=11
N=16879446, 154.598s, N - это сколько кандидатов в цепочки было передано на проверку первой ispseudoprime во всём интервале.
Проверка простых до 256 в интервале 10^37:
T:\gp64 -q M12nv.gp
180000000000000000000000000000000000000 - start
190000000000000000000000000000000000000 - stop
183880930406850062548257966254326127641: 48, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 24, 48, 24, len=11
N=19538289, 278.404s / 213.518s in PARI, N - это сколько кандидатов в цепочки было передано в PARI на проверку во всём интервале.
Далее все проверки выполняются в том же интервале, показываю только время работы.
Простые до 384: N=8914512, 153.040s / 100.044s in PARI
Простые до 512: N=5282567, 111.883s / 60.637s in PARI
Простые до 768: N=2718596, 82.486s / 32.245s in PARI
Простые до 1024: N=1717028, 70.635s / 20.842s in PARI
Простые до 1536: N=929979, 61.937s / 11.622s in PARI
Простые до 2048: N=612964, 58.756s / 7.831s in PARI
Простые до 2560: N=446093, 73.259s / 5.788s in PARI
Простые до 3072: N=347042, 58.460s / 4.727s in PARI
Простые до 3584: N=281895, 58.215s / 3.729s in PARI
Простые до 4096: N=235933, 59.634s / 3.073s in PARI
Простые до 5120: N=176715, 61.253s / 2.293s in PARI
Простые до 6144: N=141014, 61.852s / 1.982s in PARI
Простые до 8192: N=113100, 77.968s / 0.905s in PARI
Простые до 10240: N=113100, 64.382s / 1.451s in PARI
Простые до 12288: N=113100, 70.137s / 1.622s in PARI
Простые до 14336: N=113100, 65.015s / 1.591s in PARI
Простые до 16384: N=113100, 64.726s / 1.544s in PARI
Простые до 20480: N=113100, 64.780s / 1.560s in PARI
Простые до 24576: N=113100, 66.418s / 1.684s in PARI
Простые до 28672: N=113100, 67.262s / 1.528s in PARI
Простые до 32768: N=113100, 64.030s / 1.451s in PARI
Проверка влияния размера интервала перебора при вызове программы на версии с проверкой 3584 простых (выше везде использовался 10^8):
1e6: 174.190s / 6.271s in PARI
3e6: 99.232s / 4.258s in PARI
1e7: 70.175s / 3.697s in PARI
3e7: 61.668s / 3.853s in PARI
1e8: 58.215s / 3.729s in PARI
3e8: 57.470s / 3.712s in PARI
1e9: 57.971s / 3.822s in PARI




 не превышает 186778, максимальная длина такой прогрессии не больше 9. А прогрессия, начинающаяся с 186779 содержит сразу 15(!) чисел, имеющих в точности 4 делителя.
не превышает 186778, максимальная длина такой прогрессии не больше 9. А прогрессия, начинающаяся с 186779 содержит сразу 15(!) чисел, имеющих в точности 4 делителя. , а не
, а не 
 , но до
, но до  при желании.
при желании.  ) проверять делимость на большие простые (больше 8000) смысла нет, таковых вариантов просто не встретилось, остальные делители больше
) проверять делимость на большие простые (больше 8000) смысла нет, таковых вариантов просто не встретилось, остальные делители больше  . Время счёта до выхода за предел чисел уменьшилось с 7000 до 1100
. Время счёта до выхода за предел чисел уменьшилось с 7000 до 1100  на непроверяемых местах
на непроверяемых местах  ). Это не страшно, не пропуски ведь, всё лишнее отрежет PARI, влияние же на скорость незначительное (с 58с до 54с).
). Это не страшно, не пропуски ведь, всё лишнее отрежет PARI, влияние же на скорость незначительное (с 58с до 54с). в конструкции
в конструкции 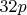 не любое нечётное, а может иметь остатки только
не любое нечётное, а может иметь остатки только  ,
,  ,
,  или
или  по модулю
по модулю  .
. индексов просчитаются за десяток секунд), но работать будет чуть медленнее (потому что AVX регистров доступно вдвое меньше и придётся больше работать с памятью). Я подумаю. Скажите если Вам это критично.
индексов просчитаются за десяток секунд), но работать будет чуть медленнее (потому что AVX регистров доступно вдвое меньше и придётся больше работать с памятью). Я подумаю. Скажите если Вам это критично. (при утроенном/ушестерённом модуле/шаге). Заранее не знал, обнаружил только что калькулятором. Про другие паттерны не скажу, не проверял.
(при утроенном/ушестерённом модуле/шаге). Заранее не знал, обнаружил только что калькулятором. Про другие паттерны не скажу, не проверял. .
. . Я тогда имел в виду, что для других паттернов и других
. Я тогда имел в виду, что для других паттернов и других  и
и  всё равно будет выполняться
всё равно будет выполняться  Закон Ньютона и здесь работает. Конечно
Закон Ньютона и здесь работает. Конечно  .
. огромных простых. А что мы про них знаем?
огромных простых. А что мы про них знаем? из них точно дают произведения:
из них точно дают произведения:  ,
,  ,
,  ,
,  ,
,  .
.




 ,
,  и получается прямо из паттерна командой chinese именно в такой форме, я уже показывал выше. Если его пересчитать в
и получается прямо из паттерна командой chinese именно в такой форме, я уже показывал выше. Если его пересчитать в  раз больше (потому что по модулю 2 и 3 допустимы лишь по единственному варианту остатка
раз больше (потому что по модулю 2 и 3 допустимы лишь по единственному варианту остатка  ) и поделить на
) и поделить на  , то получится (после одной малопонятной хитрости)
, то получится (после одной малопонятной хитрости)  ,
,  вариантов. Впрочем, считал наспех. Но порядок числа, видимо, такой.
вариантов. Впрочем, считал наспех. Но порядок числа, видимо, такой. паттернов.
паттернов.