Пока единственное ядро моего компа считает, попытаюсь написать обобщающий пост.
Во-первых, уточнение. Предлагаю считать самой перспективной концепцией КМК37-11.
Почему я удлиняю название и уточняю насчёт 11-ти:
При этом в наборах нет третьего числа, кратного 7, и вторых чисел, кратных 11 и 13 (последние теоретически могли бы присутствовать, но их допущение резко снижает эмпирическую вероятность успеха, поскольку в интересующем нас диапазоне произведения двух простых встречаются гораздо чаще, чем простые).
Ну так вот, я проговорю явно то, что может быть не замечено, как уже было. Если хоть одно из вторых чисел кратных 11 и/или 13 попадёт в паттерн, то огромных простых будет уже 12, а то и больше.
А для нас и 11 огромных простых это очень много. Пока продолжаю считать, что меньшее количество невозможно.
Жду момента, когда уважаемый
Dmitriy40, тщательно проверит все другие пути и вернётся к КМК37-11.
Также 12 дней жду ответа на этот важный вопрос:
координировать действия нескольких участников
Вот я как раз и хочу подробно разобраться, какие варианты уже проверены и какие результаты достигнуты.
Например, спрошу проверялся ли ранее тот самый паттерн, для которого
Dmitriy40 делал программу:
Код:
45p 722p 841qr 12p 49qr 50p 507p 32p 961qr 18p 605p 28p 867p 1058p 1369qr
С учетом указанных ограничений возникает несколько десятков тысяч идентичных начальных условий для программы поиска.
"Идентичные начальные условия для программы поиска" мы уже вовсю называем паттернами.
А Вы пытались рассчитать точное количество этих паттернов в рамках КМК37-11? Не о сотнях ли тысяч надо в таком случае говорить?
Я вот пытался ограничить количество самых приоритетных паттернов до

, используя новые ограничения:
На 3-м этапе брать только 28, но не 98.
На 4-м этапе брать только 605, но не 845, 1445, ..., 6845 .
Дальше есть ещё ограничения. Но обоснованность их всех пока сомнительна, да.
Тем временем комп проверил диапазон 0-500 миллиардов. И счёт в противостоянии

и

получился

. На этот раз тоже преимущество меньшего числа над большим. Но не в 8, а в 3 раза. Хотя числа, конечно, пока маловаты.

 на входе тоже нетрудно, но непонятно надо ли:
на входе тоже нетрудно, но непонятно надо ли:  , это более
, это более  :
:






 или, тем более, ровно на
или, тем более, ровно на  . А на числовой оси такие места есть только вблизи чисел кратных
. А на числовой оси такие места есть только вблизи чисел кратных  . Вот и получается, что наши планеты удалены не дальше чем на 7 единиц от центральной звезды. Они равны
. Вот и получается, что наши планеты удалены не дальше чем на 7 единиц от центральной звезды. Они равны  .
. в позиции
в позиции  неразрешимо при любых нечётных
неразрешимо при любых нечётных  ? ОК, это я понимаю, значит
? ОК, это я понимаю, значит 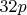 действительно обязательна.
действительно обязательна. , практически наверняка найдется искомая.
, практически наверняка найдется искомая. и свободное и получить прямые условия на 14 чисел из 15-ти. При подстановке простых
и свободное и получить прямые условия на 14 чисел из 15-ти. При подстановке простых  в указанном порядке в первый паттерн шаг (модуль) получится порядка
в указанном порядке в первый паттерн шаг (модуль) получится порядка  . Полезнее ли это пока без понятия. Моя программа работает на 30% медленнее (10с вместо 7с), но фильтрует почти вдвое лучше (2700 вместо 4700 на миллион).
. Полезнее ли это пока без понятия. Моя программа работает на 30% медленнее (10с вместо 7с), но фильтрует почти вдвое лучше (2700 вместо 4700 на миллион). и
и 

 , используя новые ограничения:
, используя новые ограничения: и
и  получился
получился  . На этот раз тоже преимущество меньшего числа над большим. Но не в 8, а в 3 раза. Хотя числа, конечно, пока маловаты.
. На этот раз тоже преимущество меньшего числа над большим. Но не в 8, а в 3 раза. Хотя числа, конечно, пока маловаты. . Тогда 6-е число
. Тогда 6-е число  , где
, где  кратно 9 и больше 9. Поэтому у 6-го числа не менне 24 делителей.
кратно 9 и больше 9. Поэтому у 6-го числа не менне 24 делителей. вариантов. Впрочем, считал наспех. Но порядок числа, видимо, такой.
вариантов. Впрочем, считал наспех. Но порядок числа, видимо, такой. раз. Это предварительно, я думаю, что исходно более 46 тысяч имеется. Прошу более подробный расчёт. Думаю по 7 этапам удобно будет рассчитать.
раз. Это предварительно, я думаю, что исходно более 46 тысяч имеется. Прошу более подробный расчёт. Думаю по 7 этапам удобно будет рассчитать.