Соплю об землю бить - не всегда уместное поведение.
Матрицу на вектор умножать - рискованное занятие. Смотрите определение векторного пространства. Конечно, матрицы формируют векторные пространства, но не это свойство делает возможным умножение матриц. Полиномы, опять же, формируют векторное простратство. Поищем корни векторов?
Который раз уже вижу эту дискуссию про то, что на что можно умножать, что нельзя умножать, кто чем является и не является (в контексте матриц и векторов). Можете объяснить, где Вы здесь проблему видите? Как я вижу - все не так уж и сложно. Матрицу можно умножать на матрицу. Векторное пространство формируют матрицы заданной размерности
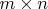
, а умножать можно любые согласованные по размеру матрицы, поэтому умножение матриц действительно не связано с тем, что они формируют векторные пространства. Является ли матрица вектором? Да является, как элемент векторного пространства матриц заданной размерности. Получается, что при умножении матриц мы умножаем 2 вектора, и что в этом такого? Если брать произвольное векторное пространство, то в его аксиоматику никакой операции умножения векторов не заложено. Проблемы с вектором и набором чисел тоже нет. Вектор - это вектор, т.е. любой элемент любого векторного пространства. Выбор базиса в конечномерном ВП индуцирует изоморфизм между этим ВП и

, тем самым вектор снабжается своими координатами - набором чисел. Сами наборы чисел могут быть векторами в прямом смысле (как элементы векторного пространства

). Что еще... Сами наборы чисел можно рассматривать как матрицы размера

или

. С теоретико множественной точки зрения - это разные вещи: матрицы - это функции, определенные на декартовом произведении некоторых отрезков натуральных чисел, а набор чисел - это элемент пространства

- упорядоченный набор элементов поля

(упорядоченные наборы определяются по-разному: либо через упорядоченные пары, либо как функции из начального отрезка натурального ряда в поле

). Разумеется между ними можно построить взаимно-однозначное соответствие. Т.е. я к тому, что здесь может быть и есть некоторая сложность на начальном этапе знакомства со всем этим, но глобальной проблемы тут никакой нету - терминология трактуется однозначно.



