Пусть к примеру многочлен состоит из произведения многочленов
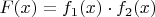
, верно ли, что эта операция приводит к объединению множеств их корней?
Из курса элементарной математики известно, что верно:
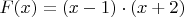
, корни

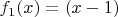
, корень

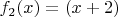
, корень
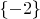
Это частный пример, но как провести доказательство для общего случая?
Доказательство:
Пусть множества
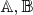
, множества корней многочленов
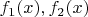
,
а

множество корней многочлена

, тогда необходимо доказать двойное включение
множеств
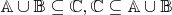
Докажем включение
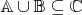
. Если
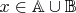
, то либо
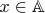
и тогда из того, что
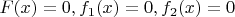
следует
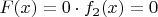
, т.е.
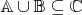
, либо же
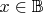
и тогда из того, что
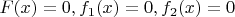
следует
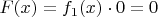
, т.е.
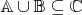
.
Теперь докажем обратное включение
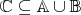
. Из доказанного выше, следует, что если
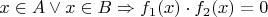
и если
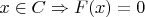
, т.е.
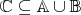
. Отсюда вывод, основное утверждение доказано.



