Задачка по Уравнениям мат. физики

[antoshka1303]

С чего вообще можно начать, чтобы решить эту систему?
\left\{ {\begin{array}{*{20}c} {\frac{{\partial ^2 u}} {{\partial t^2 }} = a^2 \Delta _2 u + k\sin (\omega t)} \\ {\left. u \right|_{\left| x \right| = R} = 0} \\ {\left. u \right|_{t = 0} = 0} \\ {\left. {\frac{{\partial u}} {{\partial t}}} \right|_{t = 0} = 0} \\ \end{array} } \right. $Где \Delta _2 = \frac{{\partial ^2 }} {{\partial x^2 }} + \frac{{\partial ^2 }} {{\partial y^2 }} \[ _{\left| x \right| < R,k = const} \]
\omega $-не совпадает ни с одной из собственных частот(отсутствует резонанс)

[незваный гость]

Попробуйте рассмотреть удовлетворяющую граничным условиям $v(x)$ такую, что ${\frac{{\partial ^2 v}} {{\partial t^2 }} = a^2 \frac{{\partial ^2 v}} {{\partial x^2 }} + k\sin (\omega t)}$. Тогда $w(x,y) = u(x, y) - v(x)$ удовлетворяет однородному уравнению ${\frac{{\partial ^2 w}} {{\partial t^2 }} = a^2 \Delta _2 w}$ (и граничным условиям).

[shwedka]

незванный гость писал(а):

:evil:
Попробуйте рассмотреть удовлетворяющую граничным условиям $v(x)$ такую, что ${\frac{{\partial ^2 v}} {{\partial t^2 }} = a^2 \frac{{\partial ^2 v}} {{\partial x^2 }} + k\sin (\omega t)}$. Тогда $w(x,y) = u(x, y) - v(x)$ удовлетворяет однородному уравнению $v(x)$ такую, что ${\frac{{\partial ^2 w}} {{\partial t^2 }} = a^2 \Delta _2 w}$ (и граничным условиям).

Ну нет, такую функцию в жизнь не найти.
Нужно перейти к полярным координатам, и, поскольку в задаче от угла ничего не зависит,
функция будет зависеть только от r,t.
Уравнение запишется в виде $u_{tt}-a^2(u_{rr}+r^{-1}u_r)=k\sin)(\omega t)$
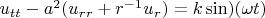
После этого в ОДНОРОДНОМ уравнении делим переменные, то есть
ищем решения специального вида, u(r,t)=T(t)F(r)
В результате для F получается уравнение Бесселя. Eго собственные функции будут $F_n(r)= J_0(r\alpha_n/R),,,, \alpha_n$ положительные нули функции Бесселя.
В заключение решение задачи ищется в виде
$ u(r,t)=\sum F_n(r ) T_n(t)$
Подаставляем в уравнение и начальные условия, для $T_n(t)$ получается уравнение
$T_n''+(\alpha_n/R)^2 T_n= C_n a^2 \sin(kt)$,'' где $C_n=\int_0^R J_0(r\alpha_n/R) r dr , T_n(0)=T_n'(0)=0$. решил и ура.

[незваный гость]

Это зависит от того, как понимать границу $|x|=R$. Я тоже сначала понял как круг, и перешел к полярным координатам. Но потом решил, что все-таки имеется в виду полоса вдоль оси $y$, и исходил из этого в решении. antoshka1303 -- выбор за Вами.

[antoshka1303]

сейчас попробую решить, у меня тоже была бысль переходить к поляцным координатам, только ия почему-то перешел к цилиндрическим...
Да, в указании я кое-что еще нашел для решения!
Указание: установить справедливость формулы

\[ \int\limits_0^x x{^' } J_0 (x{^'} )dx{^' } = x \cdot J_1 (x)} \]

и воспользоваться ею при вычислении коэффициентв ряда Фурье.
Это как раз что <b> shwedka</b> советовала!

[shwedka]

Я ошиблась немного, записывая коэффициент, один множитель забыла.
Правильно:
$C_n=\frac{\int_0^R J_0(r\alpha_n/R) r dr}{\int_0^RJ_0(r\alpha_n/R)^2 r dr }$
интеграл в знаменателе, после замены переменной, $z=r/R$ есть в справочниках, учебниках (здесь важно, что $\alpha_n$- положительные нули функции Бесселя)

[antoshka1303]

незванный гость писал(а):

:evil:
Это зависит от того, как понимать границу $|x|=R$. Я тоже сначала понял как круг, и перешел к полярным координатам. Но потом решил, что все-таки имеется в виду полоса вдоль оси $y$, и исходил из этого в решении. antoshka1303 -- выбор за Вами.

так что выбирать: круг или полосу???

[shwedka]

Да круг, круг. Ведь в условии стоят $x_1, x_2$ а тогда $x=(x_1,x_2), \;|x|=\sqrt{x_1^2+x_2^2}$.
Если бы была полоса, то записали бы $|x_1|=R$.
а игрека никакого нет!!!

[незваный гость]

shwedka писал(а):

Да круг, круг. Ведь в условии стоят $x_1, x_2$ а тогда $x=(x_1,x_2), \;|x|=\sqrt{x_1^2+x_2^2}$.
Если бы была полоса, то записали бы $|x_1|=R$.
а игрека никакого нет!!!

Вашими бы устами да мёды пить. Из самого первого сообщения:

Цитата:

$\Delta _2 = \frac{{\partial ^2 }} {{\partial x^2 }} + \frac{{\partial ^2 }} {{\partial y^2 }}$

А вот где Вы увидели $x_1$, $x_2$ -- не знаю.

Я, впрочем, не настаиваю на том, что это -- полоса. Я плохо знаю традиционные обозначения. А лапласиан меня смутил.

[shwedka]

Виновата, затмение. Но еще довод в пользу круга:
Там говорят о собственных частотах, а в полосе спектр непрерывный, собственных значений нет.

[antoshka1303]

незванный гость писал(а):

:evil:

shwedka писал(а):

Да круг, круг. Ведь в условии стоят $x_1, x_2$ а тогда $x=(x_1,x_2), \;|x|=\sqrt{x_1^2+x_2^2}$.
Если бы была полоса, то записали бы $|x_1|=R$.
а игрека никакого нет!!!

Вашими бы устами да мёды пить. Из самого первого сообщения:

Цитата:

$\Delta _2 = \frac{{\partial ^2 }} {{\partial x^2 }} + \frac{{\partial ^2 }} {{\partial y^2 }}$

А вот где Вы увидели $x_1$, $x_2$ -- не знаю.

Я, впрочем, не настаиваю на том, что это -- полоса. Я плохо знаю традиционные обозначения. А лапласиан меня смутил.

А чем может смутить Лапласиан?В вормуле ошибка?Да вроде нет...

[antoshka1303]

Значит все-таки круг?

[незваный гость]

antoshka1303 писал(а):

незванный гость писал(а):

... Из самого первого сообщения:

Цитата:

$\Delta _2 = \frac{{\partial ^2 }} {{\partial x^2 }} + \frac{{\partial ^2 }} {{\partial y^2 }}$

...
А лапласиан меня смутил.

А чем может смутить Лапласиан?В вормуле ошибка?Да вроде нет...

Лапласиан у Вас использует $(x,y)$ обозначения. Это наводит на мысль, что $x$ в $|x|$ -- первая координата, а не вектор. И, соответственно, область -- полоса, а не круг. Но мы не знаем, откуда эта часть условия -- может быть, Вы просто хотели сказать, что задача двумерная.

Я и сам первоначально посчитал область кругом и перешел к полярным координатам. Это более типично для таких задач, особенно учебных. Но вот $y$ в лапласиане...

[antoshka1303]

незванный гость писал(а):

:evil:

antoshka1303 писал(а):

незванный гость писал(а):

... Из самого первого сообщения:

Цитата:

$\Delta _2 = \frac{{\partial ^2 }} {{\partial x^2 }} + \frac{{\partial ^2 }} {{\partial y^2 }}$

...
А лапласиан меня смутил.

А чем может смутить Лапласиан?В вормуле ошибка?Да вроде нет...

Лапласиан у Вас использует $(x,y)$ обозначения. Это наводит на мысль, что $x$ в $|x|$ -- первая координата, а не вектор. И, соответственно, область -- полоса, а не круг. Но мы не знаем, откуда эта часть условия -- может быть, Вы просто хотели сказать, что задача двумерная.

Я и сам первоначально посчитал область кругом и перешел к полярным координатам. Это более типично для таких задач, особенно учебных. Но вот $y$ в лапласиане...

а, понял,конечно, имелось в виду лапласиан от x_1 x_2

[незваный гость]

Тогда -- круг и полярные координаты.