
Покажем, что в любом непустом подмножестве множества натуральных чисел имеется минимальный элемент.
Пусть

. Если

, то

, поскольку


.
Пусть теперь

, т. е.

. В множестве

должно найтись такое натуральное число

, что все натуральные числа, не превосходящие

, лежат в

, а

. Если бы такого

не было, то множество

, содержащее единицу, вместе с

содержало бы и
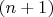
и по принципу индукции совпадало бы с

. Последнее невозможно, поскольку

.
Вопрос касательно "Если бы такого

не было, то множество

, содержащее единицу, вместе с

содержало бы и
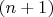
" Я лишь могу понять эквивалентное предположению от противного
![$\forall n\in E([\forall n'\in\mathbb{N} (n'\leqslant n\to n'\in E)]\to (n+1)\in E)$ $\forall n\in E([\forall n'\in\mathbb{N} (n'\leqslant n\to n'\in E)]\to (n+1)\in E)$](https://dxdy-02.korotkov.co.uk/f/1/3/f/13f202b023f083511b2b1749de539d4d82.png)
. Но в некоторых множествах, очевидно, найдутся элементы меньшие чисел, не лежащих в этих множествах. Значит
![$\forall n\in E[\forall n'\in\mathbb{N}(n'\leqslant n\to n'\in E)]$ $\forall n\in E[\forall n'\in\mathbb{N}(n'\leqslant n\to n'\in E)]$](https://dxdy-02.korotkov.co.uk/f/1/1/9/119c7cc50eb234edc907b67ff3fe967982.png)
не получим. Как тогда получили


?



