Сходимость по вероятности и в среднем

[Khomie]

Добрый вечер, уважаемые!

Вчера преподаватель задал необычную задачу: привести пример, показывающий, что из сходимости по вероятности не следует сходимость в среднем порядка $p>0$

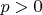
И вроде в общем и целом ничего в этом необычного нет. Сплошь и рядом валяются примеры на то, что из сходимости по вероятности не следует сходимость почти наверное и так далее, но
я лично нигде еще не встречался с таким утверждением относительно среднего порядка $p>0$.

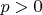
Были попытки воспользоваться обобщенным неравенством Чебышева для функции $g(x)=x^p$:
$P(\left\lvert\xi_n-\xi\right\rvert\geqslant\varepsilon)\leqslant\frac{\mathbf{E}\left\lvert\xi_n-\xi\right\rvert^p}{\varepsilon^p}$
Но это лишь оценка сверху, причем требующая, чтобы выполнялась сходимость в среднем.

Поэтому мне кажется, что нужно действительно построить какой-то пример случайной величины, которая будет сходиться по вероятности, но будет расходиться в среднем. При этом, её мат. ожидание должно существовать.
В интернете наткнулся на следующий контрпример:
$X_n=e^n\mathcal{I}_{0,1/n}$
Но врать не буду, я не понимаю, что имеется в виду. Если $\mathcal{I}$ тянет на событие-индикатор, то я не совсем понимаю, в какой именно момент оно "срабатывает".

Буду благодарен за любые ценные идеи и советы.

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);
- отсутствуют собственные содержательные попытки решения задачи.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Pphantom]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (М)»

[Otta]

Khomie в сообщении #1493151 писал(а):

Буду благодарен за любые ценные идеи и советы.

Совет: взять уже готовый подсмотренный пример (не самый удачный, но подходящий), и проверить на нем определения того и другого.

[StaticZero]

Otta, вангую вопрос номер два, как выдумать другой пример

[Otta]

Ой все, молчу.

[mihaild]

Khomie в сообщении #1493151 писал(а):

Если $\mathcal{I}$ тянет на событие-индикатор, то я не совсем понимаю, в какой именно момент оно "срабатывает".

Тут очевидно имеется в виду отрезок $[0, 1]$ с мерой Лебега в качестве вероятностного пространства, и $\mathcal{I}_{x,y}$ - индикатор отрезка $[x, y]$ (случайная величина).

Вообще чтобы легко придумывать такие примеры, полезно смотреть, на что "обращает внимание" тот или иной вид сходимости, а на что - нет. Например для сходимости по вероятности неважно, отличается величина от предельной в какой-то точке на $1$ или на $100$, а для сходимости в среднем - важно. Так что можно попробовать взять какой-то нетривиальный пример сходимости по вероятности (какой-нибудь приходит в голову?) и увеличить значения величин так, чтобы исчезла сходимость в среднем.

[Dan B-Yallay]

(Оффтоп)

mihaild в сообщении #1493177 писал(а):

Так что можно попробовать взять какой-то нетривиальный пример сходимости по вероятности (какой-нибудь приходит в голову?) и увеличить значения величин так, чтобы исчезла сходимость в среднем.

А потом понять, что вот же он:

Khomie в сообщении #1493151 писал(а):

В интернете наткнулся на следующий контрпример:
$X_n=e^n\mathcal{I}_{0,1/n}$

[StaticZero]

(Оффтоп)

mihaild, большое спасибо

[Khomie]

mihaild в сообщении #1493177 писал(а):

Khomie в сообщении #1493151 писал(а):

Если $\mathcal{I}$ тянет на событие-индикатор, то я не совсем понимаю, в какой именно момент оно "срабатывает".

Тут очевидно имеется в виду отрезок $[0, 1]$ с мерой Лебега в качестве вероятностного пространства, и $\mathcal{I}_{x,y}$ - индикатор отрезка $[x, y]$ (случайная величина).

Вообще чтобы легко придумывать такие примеры, полезно смотреть, на что "обращает внимание" тот или иной вид сходимости, а на что - нет. Например для сходимости по вероятности неважно, отличается величина от предельной в какой-то точке на $1$ или на $100$, а для сходимости в среднем - важно. Так что можно попробовать взять какой-то нетривиальный пример сходимости по вероятности (какой-нибудь приходит в голову?) и увеличить значения величин так, чтобы исчезла сходимость в среднем.

Простите мне мое невежество, Вы и так достаточно подробно мне все постарались обьяснить, но мне все равно непонятна ситуация с этим индикатором.
Как это сформировалось у меня голове: событие-индикатор - это такое событие, которое равно единице, когда происходит какое-то интересующее нас событие и нулю в противном случае.
Собственно, я, например, понимаю событие $X_n\in[0,\frac{1}{n}]$, тогда индикатором стало бы событие попадания $X_n$ в указанный интервал. Что же значит событие-индикатор отрезка пока остаётся загадкой для меня.

[Otta]

Khomie
Графики функций соответствующих порисуйте. Тут, в общем, тервер как-то побоку, тут и анализа хватит, слегка расширенного.

[alisa-lebovski]

Имеется в виду следующее. Пусть есть случайная величина $U$, равномерно распределенная на отрезке $[0,1]$. Тогда определим $X_n=e^n$, если $U<1/n$, и $X_n=0$ иначе.

[mihaild]

(Оффтоп)

Dan B-Yallay в сообщении #1493179 писал(а):

А потом понять, что вот же он

Это было к "а как такой придумать".

Khomie в сообщении #1493211 писал(а):

событие $X_n\in[0,\frac{1}{n}]$,

Это не событие, это элементарный исход (иногда называемый элементарным событием, но ИМХО это неудачная терминология - как раз путаемся с событиями).

Khomie в сообщении #1493211 писал(а):

индикатором стало бы событие попадания $X_n$ в указанный интервал

А это вообще непонятно что.

Khomie в сообщении #1493211 писал(а):

Что же значит событие-индикатор отрезка

Ничего. Индикатор отрезка - это не событие, это случайная величина.
Случайная величина - это функция, определенная на вероятностном пространстве. И у нас как раз такая функция:

$$\mathcal{I}_{A}(x) = \begin{cases} 1, x \in A\\ 0\end{cases}$$

[Khomie]

alisa-lebovski в сообщении #1493214 писал(а):

Имеется в виду следующее. Пусть есть случайная величина $U$, равномерно распределенная на отрезке $[0,1]$. Тогда определим $X_n=e^n$, если $U<1/n$, и $X_n=0$ иначе.

Хорошо, я попробую тогда привести свое решение, поправьте меня, если не сложно.

Если $U$ распределена равномерно на отрезке $[0,1]$, тогда определим $X_n=e^n\mathcal{I}\left\lbrace U\in[0;\frac{1}{n}]\right\rbrace$.
Так как $U$ распределена равномерно, то вероятность элементарного исхода $X_n=e^n$ равна $\frac{1}{n}$, а вероятность $X_n=0$ соответственно $1-\frac{1}{n}$.
Тогда, с ростом $n$ множество $X_n$ отличных от нуля стремиться к нулю и последовательность $X_n$ сходится по вероятности к $X=0$.

Следовательно, существует $\mathbf{E}X=0$.
При этом, $\mathbf{E}X_n=\frac{\exp n}{n}$, следовательно
$\mathbf{E}\left\lvert X_n-X \right\rvert ^p= \mathbf{E}\left\lvert X_n \right\rvert ^p = \frac{\exp np}{n} \to \infty$, при $ n \to \infty $
Поэтому сходимости в среднем при $p>0$ нет.

[mihaild]

Khomie в сообщении #1493250 писал(а):

вероятность элементарного исхода $X_n=e^n$

Только "события". Этому событию соответствует много элементарных исходов.

Khomie в сообщении #1493250 писал(а):

множество $X_n$ отличных от нуля стремиться к нулю

Это вообще что-то непонятное. Что за множество, что значит "множество стремится к нулю".
Надо так: $P(X_n > \varepsilon) = \frac{1}{n} \to 0$, значит $X_n \to X$ по вероятности.

Khomie в сообщении #1493250 писал(а):

Следовательно, существует $\mathbf{E}X=0$.

Непонятно, почему "следовательно;.. Но да, $\mathbf E X$ существует.

Khomie в сообщении #1493250 писал(а):

следовательно $\mathbf{E}\left\lvert X_n-X \right\rvert ^p= \mathbf{E}\left\lvert X_n \right\rvert ^p = \frac{\exp np}{n} \to \infty$,

Это правда, но сходимость в среднем определяется не совсем так.