когда центростремительное ускорение может быть направлено куда угодно (внутрь полусферы).
Это уже не будет называться
центростремительным ускорением. Это просто ускорение тела.
Разложим вектор в ускорения в сопутствующей ИСО:

- тангенциальное ускорение, направлено вдоль вектора скорости (ось

). Определяется силой тяги, силой сопротивления воздуха и проекцией силы тяжести на ось

.
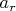
- ускорение вдоль оси корд (ось

). Определяется силой натяжения код, проекцией силы тяжести на ось


- ускорение вдоль оси

, перпендикулярно плоскости модели. Определяется подъемной силой, проекцией силы тяжести на ось

и управляющим воздействием, которое поворачивает вектор скорости в плоскости касательной к сфере (его можно считать частью подъемной силы, но тогда подъемная сила не будет перпендикулярной к плоскости модели).
Вектор кривизны, также можно разложит по этому базису. Его компонента по оси

будет нулевой (он перпендикулярен скорости).
Компонента по оси

будет описывать кривизну траектории в касательной к сфере плоскости.
А компонента по оси

будет постоянной и будет равна

Тогда в проекциях на ось

можем смело записать:


- сила натяжения кордов,

- угол между кордами и горизонтом.
Если задать необходимое натяжение как

, где

некий заданный безразмерный коэффициент больше нуля, тогда

Вот и всё. (В такой постановке задачи).
-- 03.08.2020, 20:23 --Кривизна траектории есть, а центростремительного ускорения нет.
Куда ж оно делось?
Причина "парадокса" в том, что в Вашем примере траектория самолета трехмерная, а в моем примере фигура лежит на (вертикальной) плоскости.
В Вашем примере (задача) фигура лежит на поверхности сферы, вообще-то. Вы же сами это написали и даже нарисовали.
центростремительное ускорение.
Центростремительное ускорение всегда направлено к центру окружности. По определению, которое имеется только для движения по окружности.
Поперечная же часть этого вектора всегда направлена против вектора центростремительного ускорения (увеличивает натяжение корд).
Не используйте слов, в определении которых путаетесь, пожалуйста. Можно просто написать "Поперечная же часть этого вектора всегда направлена вдоль корд (увеличивает их натяжение)."
Во-первых (и сразу во-вторых) вектора ЦСУ и натяжения корд совпадают, имеют одинаковое значение, но противоположные знаки.
Не совпадают. Центростремительное ускорение, вообще говоря, определено только по движению по окружности. То есть только тогда, когда модель движется по большому или малому кругу, а это далеко не всегда так. При этом при движении по малому кругу центростремительное ускорение совсем не будет направлено к центру сферы.
В остальных случаях говорят о
нормальном ускорении, оно направлено к центру кривизны траектории (в данной точке). Который совсем не обязан совпадать с центром сферы.
В-четвертом, я обратился за помощью, а не затем, чтобы меня елозили мордой по стеклу по каждой не принципиально-очевидной мелочи.
Это принципиальные немелочи. И меня гложут смутные сомнения, что не очевидные.



