Здравствуйте. Есть такая задача: Пусть функция

такова, что в точке

. Докажите, что

при
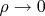
, где

.
Я понимаю, что если докажу двукратную дифференцируемость данной функции в некоторой окрестности данной точки, то дальше задача тривиально решается с применением формулы Тейлора для функции многих переменных.
Но проблема в том, что из существования второго дифференциала в точке вытекает только существование вторых частных производных в точке. Это значит, что помимо того, что первые производные существуют в этой точке в силу существования первого дифференциала, они еще и непрерывны в этой точке, ибо у них существуют производные. Тогда в силу достаточного условия дифференцируемости в точке(считаем, что она определена на каком-то множестве), сама функция

дифференцируема в точке. Однако же здесь везде речь идет только об этой точке. А двукратная дифференцируемость в точке по определению требует дифференцируемости функции в некоторой окрестности данной точки И дифференцируемости частных производных в самой точке. Т.е. я не могу получить эту окрестность и выйти на использование формулы Тейлора.
Есть формула Тейлора-Пеано, но и она потребует двукратной дифференцируемости функции в точке, так что проблему она не решает.



