svvСначала я питался в явном виде выразить изменения косинуса угла который отсекает отрезок от пустого фокуса эллиптической орбиты до планеты (аналог экванта Птолемея, хотя у него там вокруг эксцентра по идее все вращалось), в зависимости от аналогичного косинуса угла в фокусе где Солнце в явном виде. Не получилось.
Потом я понял что в абзаце книге говориться таки о бесконечно малом треугольнике который основание стоит на эллипсе который стал на это время окружностью, а не то что это треугольник на секториальном круге. После этого всего, мне удалось понять что малейшее изменение формы орбиты с круговой к эллиптической (забываем о расположении), приводит к достаточно сильной неравномерности движение, а причина в том что, я это понял с подсказок людей, что в формулу для потенциальной энергии, точнее ее максимального и минимального значения входит фокусное расстояние

, а через закон сохранение — это все связанно с кинетической энергией, какой кстати интересный этот закон сохранения энергии, просто к слову. Фокусное расстояние очень сильно зависит от малейших изменений в форме эллипса, например если зафиксировать главную полуось, и чуточку сжать меньшую полуось, всего на пару процентов, мы сразу же получим огромное расстояние между фокусами по причине что функция зависимости оного в данном случая, от малой полуоси, моментально злетает вверх при малейшем отклонении от окружности (черная линия на рисунке), в которой обе полуоси равны.
 wrest
wrestНе пойму почему это точка

не можем быть ближе чего-то там из-за направления силы? Что за апоцентр и к чему та гиперболы с параболами? Не обязательно же проводить высоты в обще стороне, можно к двум равным сторонам с точки

, равность этих высот это тоже будет условие равности площадей треугольников!
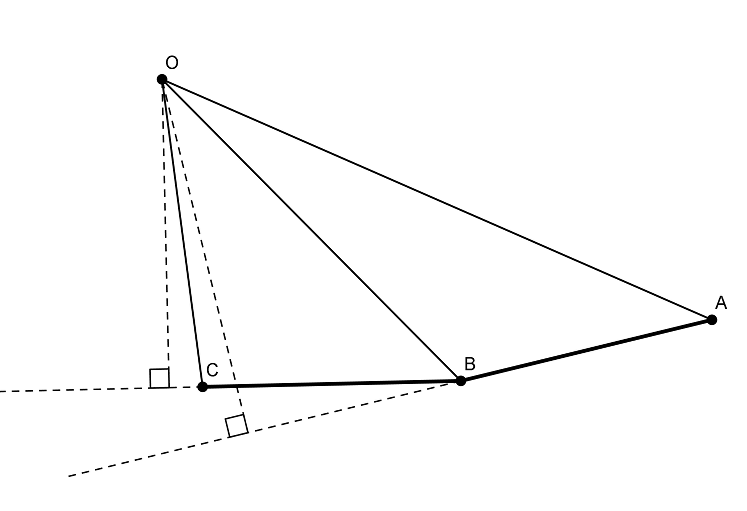
Нам остается только найти условие при котором эти высоты равны, я и пытался сделать на рисунках выше с помощью окружностей, ромбиков и хорд, но у меня пока не получилось.
Теперь проведем высоты к общей стороне, как говорили Вы.
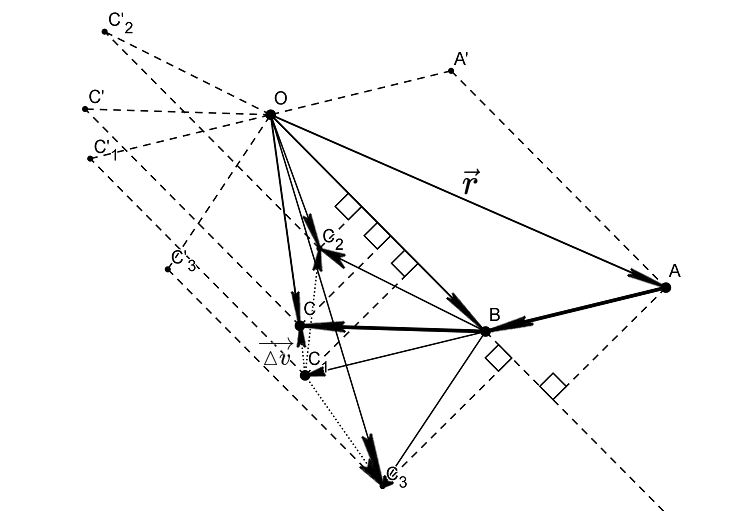
И да, действительно по определению средней скорости, при единичных промежутках времени

теперь куда направлено смещение скорости

если выходить с рисунка? Только в одной точке, ну если не считать случай когда оно нулевое, в точке —

оно параллельное радиус-вектору

. Симметрический случай будет при отдалении объекта. При этом площади треугольников

и

не равны, как и не равны площади соответствующих паралелограммов

и

, вектор

есть параллельный перенос вектора

. Если искать нечто, что соответствует условиям параллельности радиус-вектора и вектора смещения скорости, то нам нужно для начала задать эти условия из имеющихся, а именно вспоминая из векторного анализа что векторное произвидения двух векторов, если они параллельны, будет нулевым, отсюда и правила отнимания векторов по треугольнику может выйти

с этого наверное как-то траекторию можно получить, но я особо не понимаю как. И есть определение центрально сила что оно постоянно направлено к центру, то есть некой точке там? Из-за этого (я вспоминаю университет немного), не учитывается вся земля что сверху при задачи "падения Алисы к центру Земли"? Имею ввиду там что-то мне научный когда-то говорил за теорему Гаусса-Остроградского, как ее принято называть в СНГ.
П. С. Все короче надо повторять, и вектора и матан, а я чете "зависаю" как мой Семпрон 140 на новых программах для рисования геометрии, ток я на школьных задачах, ну ладно...



