Из книги В. Серпинского «Что мы знаем и чего не знаем о простых числах» ((Москва - Ленинград: Государственное издательство физико-математической литературы, 1963, стр. 14) :
"В связи с теоремой 3 заметим, что в 1850 г. П. Л. Чебышев доказал более сильную теорему (так называемый постулат Бертрана), согласно которой для натуральных

между

и
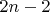
содержится хотя бы
одно простое число. Отсюда следует, что в теореме 3 число

можно заменить числом

. В настоящее время имеется элементарное доказательство этой теоремы, но оно довольно длинное [W. Sierpinsski, Arifmetyka teoretyczna, Wyd. 2, Warszawa, 1959, str. 88-94], [1]. Можно также доказать, что для натуральных
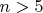
между

и

содержится по меньшей мере
два простых числа [W. Sierpinsski, Teoria liczb, II, Warszawa, 1959, str. 400], [2]."
Из книги Бухштаба «Теория чисел»:
"2.3 Теоремы Чебышева.
... В следующем утверждении, носящем название «постулат Бертрана», по-существу содержится оценка сверху расстояния между двумя соседними простыми числами

и
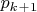
. Оно, в частности, утверждает, что
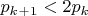
. Эта, и даже более сильная, теорема впервые была доказана в 1852 г. П. Л. Чебышевым.
Теорема 2.4. Для любого натурального

существует простое число

, удовлетворяющее неравенствам

."
Вопрос: по меньшей мере
одно или
два простых числа содержится между

и

?
Может кто сталкивался с этим вопросом. И не удаётся пока найти, скачать книги [1], [2].



