Подсказка - аксиоматика теории множеств не связана с тем, какие объекты включаются в множество.
Подсказка: на самом деле, связана. Есть такие аксиоматики, в которых объекты могут быть сами только множествами. В таких аксиоматиках "множество яблок" рассматривать некорректно, а "множество точек" - корректно только в том смысле, если сами точки дефинированы как множества.
-- 16.08.2019 14:39:09 --И я задумался, стоит ли мне и в будущем продолжать неосторожно юзать термины, или уже подходить к этому более щепетильно?
1. Вообще неосторожно юзать термины не стоит. Термины имеют смысл, и не зря они имеют какой-то сложный и тщательно оговорённый смысл. Если использовать термин неправильно, то можно сказать совсем не то, что хочется сказать.
2. Подходить слишком щепетильно - это удел педантов. Можете считать, что вам не стоит оступаться в присутствии таких, как
Brukvalub. К счастью, довольно много людей больше стремятся помочь, чем попридираться.
Ну и конечно, стоит сдерживать коней, когда хочется "уесть" собеседника. Уж вы-то меньше понимаете в множествах, чем Brukvalub, так что приводить ему такой пример не стоило.
3. Ищите "золотую середину". Да, разговаривая о математике, надо уделять больше внимания точному смыслу слов и нюансам различий разных терминов. Больше, чем вы привыкли. Но ввязываться в споры о придирках тоже не стоит, потому что это неконструктивно. Это не продвигает вас вперёд, а заставляет топтаться на месте.
-- 16.08.2019 14:58:41 --Worm2 написал правило №2. В нем для меня приятная неожиданность. Пытаясь раскусить алгоритм самостоятельно, я несколько раз подозревал, что здесь может быть замешан дистрибутивный закон, но где - понять не повезло. Правило №2 - это натуральный дистрибутивный закон, ведь так? Значит, нет сомнений что

,

,

имеют общий делитель. И тут мысль: если
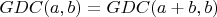
, тогда

. И снова,
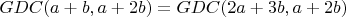
. И так до бесконечности!
Вам надо было обратить внимание на последний элемент того, что написал
worm2: тот же самый общий делитель имеет и

(здесь считаем, что

чтобы это число снова было положительным, хотя это пока и не принципиально).
А значит, цепочку можно продолжать так: этот же общий делитель имеет и
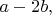
и

... (пока считаем все эти числа положительными).
И наконец, мы напишем

такое, что меньше его сделать вычитанием

уже нельзя - будет отрицательное число. И вот этот результат по определению есть остаток от деления

на
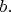
То есть,
остаток от деления будет иметь тот же общий делитель, что и исходные числа.
И дальше Алгоритм Евклида состоит в повторении этого снова и снова - но общий делитель при этом всё равно сохраняется и у новых чисел, и у двух самых первых. Как бы далеко мы ни зашли. Но "до бесконечности" мы зайти не можем: наши числа всё время уменьшаются, оставаясь целыми, а значит, рано или поздно упрутся либо в 0, либо в 1 (и тогда всё равно в 0).



