Добрый день.
Необходимо определить предельную погрешность КФ

, если изместны предельные погрешности подынтегральных функций.
Конкретика: имеем два сигнала. У них известно значение максимальной погрешности зависящее от дискретности задания этой ф-ции.
Вычисляю ВКФ этих функций.
Как оценить погрешность уже ВКФ - ума не приложу.
Если, например, заменить упрощенно интеграл на сумму, то каждая (табличная) точка (произведение

)будет иметь относительную погрешность равную сумме относительных погрешностей каждого из множителей.
Примечание - Если есть две величины  и
и  , у каждой из которых известна относительная погрешность
, у каждой из которых известна относительная погрешность 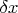 и
и  , то величина равная произведению этих величин будет иметь относительную погрешность равную
, то величина равная произведению этих величин будет иметь относительную погрешность равную  .
.
Далее. Сумма предполагает, что абс. погрешность суммы есть сумма абс. погрешностей слагаемых.
И вот дальше как-то выделить общий случай - не ясно как, т.к. длина функции в общем случае разная, а след-но разное кол-во слагаемых. Т.е. как выразить погрешность

через погрешности

?
Если перейти к относительной погрешности, то отн. погрешность остается для суммы такой же как и для отдельного слагаемого. Казалось бы проще становится на перый взгляд. Но как тогда прикинуть сумму, амплитуда же в каждой точке разная. Вобщем пока в голове сумбур, просьба помочь хоть комментариями, может что и придумается.
PS: Прошу прощения, я описывал не строго математическими наверно терминами. Наверняка тут много к чему можно подкопаться, но я пытался суть передать, а не выдержать строгую терминологию, тем более вряд ли я смог бы наверно это сделать. )))



