Работает, но надо эти команды ставить между тегом math и долларом внутри него.
О! Спасибо еще раз! А то я перепробовал эти программы размера а оно ни в какую... Теперь посты с формулами будут покрасивей, такие как мне нрявятся.
В аспиранты - могут. Формально там достаточно вступительных экзаменов в аспирантуру. Ну, в зависимости от места, могут потребовать рекомендации в аспирантуру от кого-нибудь (от организации). Например, в вузе обычно краснодипломникам дают рекомендацию, и организуют таким образом конвейер из студентов в аспиранты того же вуза. Но бывают и аспирантуры независимые, например, у какого-нибудь НИИ.
Но неформально, хорошо бы перед подачей документов и сдачей экзаменов как-то познакомиться с этими людьми, чтобы они вас захотели. Лучше всего - заранее договориться с научруком о руководстве и теме. При этом можно быть ни бум-бум в теме, он вас поначалу просто как ломовую лошадь подручного работника будет использовать. Но это, опять же, зависит от места, человека и ситуации.
Ну я думаю если под тридцать, это не поздно? Я просто не знаю сколько лет мне понадобится чтобы, как говорят, повторить то что не знал да еще и забыл... Я хочу по универах искать научного руководителя на аспирантуру уже когда немного подучу, а то как-то стыдно, я так не могу. В мечтах сначала было типа статью написать, а потом уже со статьей чапать, но это слишком сложно.
Насколько я в курсе, сильно постсоветскую систему тут нигде не ломали. В РФ введена система "бакалавр-магистр", но это для студентов. И введён "список журналов ВАК". Другие крупные изменения в голову не приходят.
Да, вроде ничего не изменилось, экзамен по специальности и мо языку. И приветствуется куча всяких рекомендаций в идеале публикаций... Только новое узнал что аспирантура бывает платная!
Смело? Такого не бывает

Но вообще, хорошо бы уровень выпускника вуза по специальности. Причём:
1)
свежего выпускника, а не "10 лет назад" - со временем без использования навыки сильно деградируют;
2) не абы какого выпускника, а хотя бы верхней трети. Может быть, верхних 10 % или 5 %. От места зависит.
(Такие выпускники ещё в студентах часто слушали доп. курсы, занимались самостоятельной работой - публикации, контакты с потенциальными научруками. Но это всё неформально.)
А вот на физиков которым не надо быть в лабораториях днями (теоретиков), чтобы мне получить самобучением (и повторением) нужный,
минимальный такой проходной уровень, это долго надо учится? Ну примерно конечно все, так...
Вы как-то систематически путаете бумажку с реальными навыками. Если есть бумажка, но навыков нет - вы никому не нужны и ничего на этом не заработаете. А если навыки есть, но нет бумажки - то никто на это и не посмотрит.
Это хорошо!
О! Вот это великий навык! Я его очень ценю! И стараюсь требовать (к сожалению, неформально). Хуже нет зрелища, чем человек, который тужится воспроизвести

из конспекта, который он же тужился срисовывать с доски. Или ещё страшнее, когда человек путает

и

Не, ну я так, шутя. Имел ввиду что я не полностью нолевой был в универе, и оценки, пусть и тройки, в основном не просто так ставили. И да, немного запомнился алфавит греческий.
Слушайте, чё вы с такими знаниями на параболах топчетесь?
Пара вопросов для проверки.


Да потому-что у меня систематически, подряд, скурпулезно ничего не получалось учить, и поэтому я зависаю на очевидных вещах, элементарных, просто потому, что именно эту вещь, когда-то во время школы или универа просто прошляпил... Хочу хоть раз подряд это все.
Ух, без подсматривань в гугл, так сразу, я просто еще до электродинамики не дошел по повторении... Но, это не водокачка нарисованная, видите, могу отличить...

Даже могу сказать что это записано в системе Гаусса, и что смысл нулевой дивергенции вектора магнитной индукции есть в отсутствии магнитных зарядов, то есть монополей магнитных, ток по аналогии должна быть напряженность магнитного поля. Еще эти уравнения выражают эмпирические законы распостранения электрического тока в проводнике например, по идеи то что напряженность электричесного поля создает ток с плотностью заряда (кстати не пойму смысла плотности заряда)
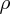
это закон Ома, так как в нем связаны напряжение и создаваемый ток с сопротивлением. Векторное произвидение градиента на вектор напряженности, дает переменное во времени (скорость этой перемены) магнитное поле, это смысл закона индукции, если тепебить в пространстве что-то, что имеет электрическое поле, то в результате можно получить магнитное поле. Вот последние уравнение напоминает мне фамилию Фарадей, но вспомнить закон чет так сразу не выходит. Что такое

? Плотность поверхностных зарядов?

П. С. Кстати когда я добавил "\large", перестало работать "\begin{aligned} \end{aligned}", и центрирование, и даже когда я убрал это "\large", выравнивание опять работать не стало...



