Отсюда следует, что существует такая матрица

, что

, где

.
И что при помощи этой матрицы любую метрику можно заединичить во всём пространстве.
А вот то, что у Вас дальше это не "то есть". Дальше возникает вопрос. Будет ли матрица

матрицей преобразования координат.
Матрица преобразования координат определяет 4 дифференциальных уравнения.
Неверно!
Чтобы прочувствовать вопрос насчет диагонализации, вы должны прорешать конкретные задачи.
Пусть хотя бы в двухмерном случае.
Вот например, возьмите конкретную метрику

(или

, если объединить симметричных членов).
Нужно найти преобразования координат

такие, чтобы в новых координат

та же метрика имела диагональный вид.
(Обычно вместо

пишут просто

и соответно вместо

,

пишут

,

подразумевая что "старые координаты"

это функции из "новых"

- но я пока буду здесь обозначать функции отдельными именами).
Тоесть: дано

, ищем неизвестные функции

такие - чтобы метрика в новых координат

имела диагональный вид.
Я взял эту метрику наобум, с потолка (непонятно то ли поверхность кривая, то ли координаты кривые, то ли и одно и другое - но это нам пока не важно - задача обратить в диагональном виде хотя бы как-нибудь) - оказалось, найти решение легко в аналитичном виде (при этом оно неоднозначно, существуют самые разные решения).
Решили?
Что вы делали, как подходили?
Напишите также какие конкретные преобразования получили для

.
-------------------
Теперь, давайте в общем виде (опять для двухмерного случая).
Пусть у нас дана двухмерная метрика в общем случае

или eсли объединить диагональные элементы из-за симметрии

что то же самое (хотя чтобы ощутить паттерна в записей, лучше не объединять а просто помнить что они одинаковы)
Нужно найти преобразования координат

такие, чтобы в новых координат

та же метрика имела диагональный вид.
Тоесть: даны три известные функции от

и

:

,

,

Ищем функции

такие - чтобы метрика в новых координат

, та же имела диагональный вид.
Что тут дано? Даны три функции

из

- или что то же самое, из

.
Что ищется? Две неизвестные функции

из

такие, чтобы в той же метрике в новых переменных диагональный член (функция-множитель перед

) был равен нулю.
Из

сразу находим


Теперь нужно просто подставить

и

в исходную метрику, раскрыть скобки, и сгруппировать множители перед произведений дифференциалов

и

.
Также функции

можно переписать просто как

.
Проделайте это руками, на бумаге - найдите всех метрических коеффициентов метрики в новых координат - вы ощутите что тут есть паттерн (и поэтому сокращенная запись суммирования Эйнштейна позволяет записать эти суммы очень компактно - что здесь я не делаю).
(Например, что должно получиться для диагонального члена  , т.е. множителя перед
, т.е. множителя перед  той же метрики в новых переменных)
той же метрики в новых переменных)
Тоесть, чтобы привести метрику в диагональным виде (внедиагональный член метрики обнулился - "сделать метрику диагональной во всем пространстве"), мы имеем
одно уравнение в частных производных первого порядка, для
двух неизвестных функций из двух переменных

которые ищем, типа

Уравнение
одно, потому что в двухмерном случае есть только один внедиагональный член метрики (их на самом деле два, но из-за симметрии они равны).
Неизвестные функции
две, потому что в двухмерном случае у нас две координаты (и соответно
две неизвестные функции перехода к новых координат)
Итак, видно что
в двухмерном случае задача недоопределена (у нас "одно уравнение" на "двух неизвестных").
Это дает возможность легко подобрать решение для преобразований, притом не единственным способом.
Например, мы можем положить для одного из преобразований просто

, или

- уравнение упростится в виде

что уже одно уравнение одной функции в частных производных, и соответно имеет единственное решение для
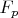
(зависящее от одной произвольной функции на граничных условий)
Теперь, должно быть легко прикинуть что будет в четырехмерном случае.
Чтобы обнулить все диагональные коеффициенты новой метрики тождественно - "сделать метрику диагональной во всем пространстве" - у нас будут
целых шесть уравнений в частных производных первого порядка, связывающие
только четыре неизвестных функций и их частных производных.
В общем случае для четырехмерного случая ясно, что теперь
задача переопределена (уравнений больше чем неизвестных) - тоесть решений (таких функций) вообще может и не быть.
Значит, в четырехмерном случае не всегда можно перейти к метрическим тензором диагонального вида, путем преобразования координат.
-- 21.03.2019, 21:12 --manul91
Спасибо! А то я думал, только рассуждениями о разрешимости ДУ можно. Не догадался компоненты посчитать.
Ну, это по сути те же рассуждения о разрешимости ДУ.
Для обращения

независимых компонентов метрики в наперед требуемом виде (в частности - обнулить все внедиагональные компоненты) - это

(нелинейных) уравнений в частных производных первого порядка, из

неизвестных функций - где

размерность пространства, а

к-во независимых членов метрики которые мы хотим обратить в конкретном виде (в частности, количество независимых внедиагональных членов равно

).