Действительно, в книге Арнольда есть доказательство. Но оно там в середине, и, как обычно у Арнольда, труднопонимаемо. Приведу доказательство, использующее обычный матан (но следующее той же основной идее; есть и основанные на других идеях).
Пусть

,

. Рассмотрим функцию

т.е.

--- кусочно-линейная, и периодическая с периодом

. В точках

(

) равна

,

--- нулю.
Пусть

--- ее ряд Фурье. Поскольку

удовлетворяет условию Дини равномерно на
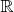
, то ее ряд Фурье сходится к ней равномерно. Ясно, что мы можем рассматривать ее как функцию на окружности

. При этом

Теперь пусть

. Для произвольных

,

можно рассмотреть функцию

Перемножая ряды Фурье (и их отрезки) для

, видим, что ряд Фурье для

равномерно сходится к ней на

. Следовательно, верно
Предложение. Для любых  ,
,  , и
, и 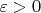 существуют
существуют  и числа
и числа  , где
, где  пробегает мультииндексы, подчиненные условию
пробегает мультииндексы, подчиненные условию  , такие, что
, такие, что  всюду на
всюду на  . Здесь
. Здесь  . При этом
. При этом  .
. 
( Здесь и ниже

означает сумму по мультииндексам, подчиненнным указанным условиям. )
-- 24.02.2019, 21:06 --Затем нам понадобится
Лемма.  где
где  есть расстояние до ближайшего целого числа. Доказательство
есть расстояние до ближайшего целого числа. Доказательство следует из соотношения
 Теорема. Пусть
Теорема. Пусть  , где
, где  и линейно независимы над
и линейно независимы над  . Тогда множество
. Тогда множество  всюду плотно в
всюду плотно в  . Доказательство.
. Доказательство. Допустим противное. Тогда существует точка

, некоторая окрестность которой не содержит точек вида

. Следовательно, для некоторого

имеем

, для любого

, где

.
Возьмем

. Пусть

где

,

--- коэффициенты Фурье для

. Существует

такое, что


.
Рассмотрим сумму

. Это нуль. Значит

по модулю не превосходит

.
Рассмотрим внутреннюю сумму для каждого

. При

это, естественно,

. При

это

где

. Но

в

в силу линейной независимости

, поэтому сумма есть

. Постоянная в последнем

зависит от

, но, во всяком случае, таких сумм конечное число. Поэтому

Отсюда видно, что

, чего при

не может быть.
