После всех перипетий, немного неевклидовых, я бы хотел объявить о найденном камне преткновения. И даже чуть заметить в адрес задачника Батыгина-Топтыгина, что перестановка задач 208 а) и б) позволила бы проскочить обе с ходу. Но вот было бы это полезнее - едва ли. Задача (а) про пустотелый сегмент заманивает симметрией - и та ведёт к диску и интегральному уравнению. Размещение же центра инверсии на краю сферического сегмента, хоть и уничтожает симметрию, даёт решение в элементарных функциях.
Саму задачу я ещё не решил формально, но решил её для диска, а для сегмента надо только добавить одно слагаемое, которое оставляет интеграл берущимся в элементарных функциях. Так что "нерешённость" условная.
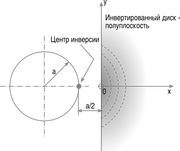
Трюк в том, что центр инверсии надо обязательно брать на краю сегмента. Тогда вместо диска получаем полуплоскость. Её преимущество в том, что получаем в своё распоряжение "бесконечность", где любой потенциал равен нулю. Этот факт позволяет избавиться от одной постоянной интегрирования при манипуляциях с уравнением Лапласа.
В моём решении есть пара "неприятных скользких" мест. Решение совпадает с известным, но я боюсь, что просто "подгоняю под ответ". Эти два места я ещё раз отмечу перед конкретными формулами. Буду искренне благодарен за подсказки.
Попытка решения задачи методом пространственной инверсии для электроёмкости диска радиуса R. - с правильным ответом, но ненадёжными рассуждениями Имеем диск радиуса

. Центр инверсии помещаем на краю диска. Радиус инверсии принимаем равным

. Диск превращается в полуплоскость, кромка которой находится на расстоянии

от центра инверсии. Эскиз нарисован наспех в графическом редакторе мышью. Прошу извинить за халтуру.
Получаем задачу - найти потенциал, создаваемый зарядами плоскости в ответ на заряд

в центре инверсии, который берут численно равным "минус

"
Про то, что

позвольте пропустить. Потенциал индуцированных зарядов на плоскости

Касательная компонента поля Е (точнее, абсолютная величина касательной компоненты)

Дальше "скользкость №1". Я подменяю

на

. Модуль вектора, конечно, скаляр, но подмена нехорошая. Дальше, из уравнения Лапласа, я делаю скоропалительный вывод, что нормальная компонента
производной Е обязана быть равна касательной. Из нормальной компоненты поля Е получаю поверхностную плотность заряда,

, и остаётся только найти потенциал в точке инверсии.
Здесь "скользкость №2". Плотность интегрируется дважды - по обеим сторонам полуплоскости. Тем не менее, потенциал в центре инверсии
![\raggedright\[U_0 = \frac{1}{4\pi} \cdot 4 \int_0^{\infty} \int_0^{\infty} \frac{dxdy}{\left(x+a/2\right)^2+y^2}\] \raggedright\[U_0 = \frac{1}{4\pi} \cdot 4 \int_0^{\infty} \int_0^{\infty} \frac{dxdy}{\left(x+a/2\right)^2+y^2}\]](https://dxdy-03.korotkov.co.uk/f/a/2/6/a26d1e0c031438c1880a8099a803c0e682.png)
Интеграл совершенно безобидный, он даёт

, что после умножения/деления/сокращения с

даёт

- ёмкость диска.
Это ещё не конец, но он скоро. С уважением.



