Предельная функции распределения сумматорной ариф. функции

[vicvolf]

Lia в сообщении #1351543 писал(а):

Вместо того, чтобы мучить ряды (которые на самом деле формула Тейлора, и выполнена в окрестности нуля при известных дополнительных условиях, ряды здесь не прокатят), было бы гораздо эффективнее использовать простейшую оценку $e^z-1$. И то, что Вы хотите, получится в одно действие. Только это очень грубая оценка и при больших значениях аргумента х.ф. она ничего не даст. Как Вы ее собираетесь использовать - только Вам известно.

Тогда поясните, пожалуйста, почему Вы считаете, что можно использовать формулу $z=e^z-1$, ведь отсюда справедливо $e^z=1+z$, а следовательно, требуется дифференцируемость $e^z$, где $z$ - дискретная переменная.

[Lia]

vicvolf в сообщении #1351769 писал(а):

почему Вы считаете, что можно использовать формулу $z=e^z-1$

Откуда видно, что я так считаю?

[vicvolf]

Lia в сообщении #1351543 писал(а):

было бы гораздо эффективнее использовать простейшую оценку $e^z-1$. И то, что Вы хотите, получится в одно действие.

Как Вы предлагаете использовать эту оценку?

[Lia]

Непосредственно.

[vicvolf]

Как доказать, что простейшей оценкой $e^z-1$ является $z$ без использования производных?

[Lia]

В Вашем случае, когда $z$ чисто мнимое, простейший способ - из геометрических соображений.

vicvolf
Все-таки это дискуссионный раздел. Здесь Вы утверждаете и Вы обосновываете.
С вопросами лучше идти в ПРР, да и то спросят попытки решений.

[vicvolf]

Lia спасибо за замечание. Я подумаю над другим вариантом доказательства утверждения.

[vicvolf]

Не получилось доказать утверждение в общем виде, докажу в частном, который меня устраивает.

Утверждение 4

Пусть имеются случайные ограниченные величины $f_n$ и случайная ограниченная величина $f:f_n \to f$ (по распределению) при $n \to \infty$.

Допустим, что для математического ожидания $f_n$ выполняется:

$M[f_n]=M[f]+o(g(n))$, (15)

где $g(n)$ - убывающая функция и $lim_{n \to \infty} {g(n)}=0$.

Тогда асимптотика характеристической функции $f_n$ в окрестности $t=0$ при $n \to \infty$ равна:

$\varphi_{f_n}(t)=\varphi_f(t)+r$, (16)

где $|r | = |t|o(g(n))$.

Доказательство

На основании Утверждения 3 получим:


$|r|=|\varphi_{f_n}(t)-\varphi_f(t)|=|it(M[f_n]-M[f]) -t^2/2$$ (M[f_n^2]-M[f^2)])+...|=|t|o(g(n))$, что соответствует (16).


Кстати можно доказать при этих условиях на основании оценки $e^z=1+z$, так $z$ в окрестности $t=0$ мало.

[vicvolf]

В связи с тем, что статья пока не опубликована приведу только формулировку следующего утверждения.

Утверждение 5

Пусть имеется сумматорная функция $S(n)=\sum\limits_{k=1}^n {f(k)}$, где арифметическая функция $f:N \to R$ является ограниченной. Предположим, что для случайной величины $f_n:f_n(k)=f(k),(n=1,2,...)$ выполняются все условия Утверждения 4 с $g=1/n$. Тогда случайная величина $S_n:S_n(k)=S(k),(1 \leq k \leq n)$, а следовательно сумматорная функция $S(n)$ при $n \to \infty$ имеет нормальное распределение.

Поясню сказанное выше на примерах.

Пример 1

Рассмотрим сумматорные функции Мертенса, Лиувилля. Для указанных сумматорных функций будем использовать, принятые выше обозначения: $S(n)= \sum\limits_{k=1}^n {f(k)}$. Проверим для этих функций выполнение условий Утверждения 5.

В данном случае слагаемые функции $f:N \to R$ (Мебиуса, Лиувилля) и соответственно случайные величины $f_n:f_n(k)=f(k)$ и случайная величина $f:f_n \to f$ (на основании Утверждения 2) являются ограниченными, поэтому эта часть условия Утверждения 5 выполняется.

Далее, если справедлива гипотеза Римана, то для указанных сумматорных функций выполняется следующая оценка сверху: $S(n) =o(n^{1/2+\epsilon})$, где $\epsilon$ - малое положительное число, поэтому для разности средних значений слагаемых арифметических функций и соответственно для случайных величин справедлива оценка:

$M[f_n]-M[f]=1/n \sum\limits_{k=1}^n {f(k)}=S(n)/n=o(n^{-1/2-\epsilon})>>o(1/n)$, (26)

учитывая, что на основании Утверждения 2 значение $M[f]=0$.

Следовательно, на основании (26) данная часть Утверждения 5 не выполняется.

Поэтому на основании Утверждения 5 мы не можем утверждать, что сумматорные арифметические функции Мертенса и Лиувилля имеют предельным (при $n \to \infty$ ) нормальное распределение.

[vicvolf]

Пример 2

Сформулируем этот пример, как утверждение.

Утверждение 6

Пусть имеется знакопеременный сходящейся ряд, у которого сходятся как ряд из положительных членов, так и отрицательных членов, притом сумма ряда из положительных членов равна $\sum\limits_{k=1}^{\infty} {a_k}=A$, а сумма ряда из отрицательных членов равна $\sum\limits_{k=1}^{\infty} {b_k}=-A$. Тогда сумматорная функция, являющаяся частичной суммой данного знакопеременного ряда $S(n)=\sum\limits_{k=1}^{n}{f(k)}=\sum\limits_{k=1}^{n} {a_k+b_k}$ при $n \to \infty$ имеет предельным - нормальное распределение.

Доказательство

По условию сумма знакопеременного ряда:

$\sum\limits_{k=1}^{\infty} {a_k+b_k}=A-A=0$. (27)

Так как ряд $\sum\limits_{k=1}^{\infty} {a_k}$ сходится, то $a_n \to 0$ при $n \to \infty$. Так как ряд $\sum\limits_{k=1}^{\infty} {b_k}$ сходится, то $b_n \to 0$ при $n \to \infty$. Поэтому:

$a_n+b_n \to 0$ при $n \to \infty$. (28)

Из (28) следует ограниченность арифметической функции $f(n)=a_n+b_n$, поэтому выполняется первая часть условия Утверждения 5.


На основании (28) случайная величина $f=0,(f_n \to f)$, где случайная величина - $f_n:f_n(k)=f(k)$, поэтому она ограничена и $M[f]=0$.

Так как ряд из положительных членов сходится то для частичной суммы справедлива оценка $\sum\limits_{k=1}^{n} {a_k}=A+o(1)$. Так как ряд из отрицательных членов сходится то для частичной суммы справедлива оценка $\sum\limits_{k=1}^{n} {b_k}=-A+o(1)$. Поэтому:

$\sum\limits_{k=1}^{n} {a_k+b_k}=A+o(1)-A+o(1)=o(1)$. (29)

На основании (29) получим следующую оценку для сумматорной арифметической функции:

$S(n)=\sum\limits_{k=1}^n {f(k)}=\sum\limits_{k=1}^n {a_k+b_k}=o(1)$. (30)

Учитывая (28), (30) для среднего значения случайной величины получим оценку:

$M[f_n]=\sum\limits_{k=1}^n {f(k)}/n=M[f]+o(1/n)$,(31)

поэтому вторая часть Утверждения 5 также выполняется.

Следовательно, все условия Утверждения 5 выполнены, поэтому данная сумматорная функция имеет предельным (при $n \to \infty$) нормальное распределение.

[Lia]

vicvolf
Чтобы не отвлекаться на частности, а все остальное - частности, я повторю еще раз главное:
оставьте теорию вероятностей в покое. Вы ее изучаете - это хорошо. Но не надо пытаться ее притянуть к чему попало. У Вас если и предвидятся какие-то результаты, то это анализ. Последовательности, ряды, средние и т.д. Вот на этом языке и говорите.

Иначе читать невыносимо это надругательство над тервером, честное слово.

Оттого, что функция, определенная на множестве, меняется хаотически, как Вы выражаетесь, она не становится случайной величиной. Синус на множестве натуральных чисел очень непредсказуемо себя ведет. Но это не случайная величина, хоть двадцать раз Вы это повтори, хоть сто двадцать.

Какое нормальное распределение еще? откуда оно тут? центральную предельную теорему, поди, используете? А условия проверить?

Про мелочи я даже не хочу говорить, хотя они очевиднее, нагляднее и лежат на поверхности. Но Вы за разговор о мелочах цепляетесь, как за спасательный круг, как это с предыдущей Вашей активной темой произошло: Вам пришлось проститься с большей и главной частью заявленных результатов, но Вы продолжаете свою линию, как бы и не заметив этого.

Это тоже мелочь.
Не мелочь: оставьте тервер в покое. К гипотезе Римана он не имеет отношения.
И если так уж хотите продолжать заниматься изысканиями в области ГР, переводите Ваши утверждения на язык анализа.

[vicvolf]

Lia в сообщении #1351543 писал(а):

Выискивать ошибки не имею возможности, поэтому тему не читаю.

Я понимаю - нет времени! Но тогда не надо делать такие идеологические замечания.

Lia в сообщении #1352531 писал(а):

vicvolf
Чтобы не отвлекаться на частности, а все остальное - частности, я повторю еще раз главное:
оставьте теорию вероятностей в покое. Вы ее изучаете - это хорошо. Но не надо пытаться ее притянуть к чему попало. У Вас если и предвидятся какие-то результаты, то это анализ. Последовательности, ряды, средние и т.д. Вот на этом языке и говорите.
Иначе читать невыносимо это надругательство над тервером, честное слово.
Оттого, что функция, определенная на множестве, меняется хаотически, как Вы выражаетесь, она не становится случайной величиной. Синус на множестве натуральных чисел очень непредсказуемо себя ведет. Но это не случайная величина, хоть двадцать раз Вы это повтори, хоть сто двадцать.

А если хотите делать такие замечания, то надо читать тему сначала. Потому что в первом сообщении темы определено вероятностное пространство:

vicvolf в сообщении #1343022 писал(а):

Известно, что любой начальный отрезок натурального ряда $1,2,...,n$ можно естественным образом превратить в вероятностное пространство с равномерной вероятностной мерой $(Q_n,A_n,P_n)$, взяв в качестве $Q_n=(1,2,...,n)$, $A_n$ - все подмножества $Q_n$, $P_n=N(m \in A)/n$, где $N(m \in A)$ - это количество членов отрезка натурального, удовлетворяющих условию $m \in A$.
Тогда произвольную (вещественную) арифметическую функцию $f(k)$ для каждого $k(1 \leq k \leq n)$) можно представить как случайную величину $x_n(k)=f(k)$. Поэтому, можно говорить о математическом ожидании (среднем значении), дисперсии, функции распределения и характеристической функции $f(k)$.

Это не мною придумано, это основы вероятностного подхода к теории чисел.

Lia в сообщении #1352531 писал(а):

как это с предыдущей Вашей активной темой произошло: Вам пришлось проститься с большей и главной частью заявленных результатов, но Вы продолжаете свою линию, как бы и не заметив этого.

Основное в предыдущей теме было показать асимптотическую независимость некоторых арифметических функций, так тема и называлась. Новая тема как раз посвящена использованию этого (смотрите ссылку в том же первом сообщении темы).

[Lia]

vicvolf в сообщении #1352603 писал(а):

Но тогда не надо делать такие идеологические замечания.

Надо.

vicvolf в сообщении #1352603 писал(а):

А если хотите делать такие замечания, то надо читать тему сначала.

Совершенно ни к чему читать всю тему, чтобы убедиться в том, что ТС, не владеющий матаппаратом на уровне 1-го курса, но пытающийся лезть в дебри, с дебрями не совладает.

Выучите сперва, что такое о-маленькое. А что Вы умеете составлять лоскутные одеяла из когда-то поданных разумных Вам замечаний, я не сомневаюсь. Как, кстати, и в том, что вероятностные методы в теории чисел применяются.
Но Вы тут при чем?

-- 08.11.2018, 23:41 --

vicvolf в сообщении #1352603 писал(а):

А если хотите делать такие замечания, то надо читать тему сначала. Потому что в первом сообщении темы определено вероятностное пространство:

Вам вот тут «Вероятностное доказательство» объясняли то же самое - что вероятность притягивается там, где не используется. Какая может быть вероятность в детерминированных случаях? Вы согласились. Или забыли?
Ну вот, объясняю еще раз.

-- 08.11.2018, 23:47 --

А вообще никаких проблем. Два модератора садятся, гробят воскресенье, выписывают из Вашего текста все неграмотно составленные строки (каждая вторая навскидку), после чего тема благополучно едет по назначению.

Если Вам говорят, что читать невозможно - то значит, действительно невозможно. Обратите внимание, что никто и не читает. У людей, хоть как-то связанных с математикой, идиосинкразия на такие тексты. Инстинкт самосохранения срабатывает.

[vicvolf]

Lia в сообщении #1352733 писал(а):

Вам вот тут «Вероятностное доказательство» объясняли то же самое - что вероятность притягивается там, где не используется. Какая может быть вероятность в детерминированных случаях? Вы согласились. Или забыли?
Ну вот, объясняю еще раз.

Спасибо, что Вы помянули эту тему. Я ее прекрасно помню. Там было одно очень хорошее сообщение, которое поясняет вероятностный подход к изучению арифметических функций. Вообще это достаточно новый подход. Он сформировался окончательно в середине прошлого века с доказательством теоремы Эрдеша-Каца о нормальном распределении арифметической функции количества простых делителей натурального числа. https://ru.wikipedia.org/wiki/%D0%A2%D0 ... 1%86%D0%B0 Это сообщение было как раз об этой теореме.

RIP в сообщении #1256452 писал(а):

Теорему можно сформулировать на языке теории вероятностей. Доказательство её использует результат из теории вероятностей (теорему Леви о непрерывном соответствии между функциями распределения и характеристическими функциями случайных величин, или метод характеристических функций).

Любой начальный отрезок натурального ряда $\{1,2,\dotsc,n\}$ можно естественным образом превратить в вероятностное пространство $\left(\Omega_{n},\mathcal{A}_{n},\mathbb{P}_{n}\right)$, взяв $\Omega_{n}=\{1,2,\dotsc,n\}$, $\mathcal{A}_{n}$ — все подмножества $\Omega_{n}$, $\mathbb{P}_{n}(A)=\frac{|A|}{n}$. Тогда произвольную (вещественно- или даже комплекснозначную) функцию $f(k)$ натурального аргумента (а точнее, её ограничение на $\Omega_{n}$) можно рассматривать как случайную величину $\xi_{n}$ на этом вероятностном пространстве: $\xi_{n}(k)=f(k)$, $1\leqslant k\leqslant n$. В частности, можно говорить о мат. ожидании $\mathbb{E}\xi_{n}=\frac{1}{n}\sum_{k=1}^{n}f(k)$ и дисперсии $\mathbb{D}\xi_{n}=\mathbb{E}\left\lvert\xi_{n}-\mathbb{E}\xi_{n}\right\rvert^{2}=\mathbb{E}\left\lvert\xi_{n}\right\rvert^{2}-\left\lvert\mathbb{E}\xi_{n}\right\rvert^{2}=\frac{1}{n}\sum_{k=1}^{n}\bigl\lvert f(k)\bigr\rvert^{2}-\left\lvert\frac{1}{n}\sum_{k=1}^{n}f(k)\right\rvert^{2}$, а для вещественной $f$ — о функции распределения $F_{\xi_{n}}(x)=\frac{1}{n}\bigl\lvert\{k\leqslant n:f(k)\leqslant x\}\bigr\rvert$ и характеристической функции $\varphi_{\xi_{n}}(t)=\mathbb{E}\mathrm{e}^{\mathrm{i}t\xi_{n}}=\frac{1}{n}\sum_{k=1}^{n}\mathrm{e}^{\mathrm{i}tf(k)}$.

Таким образом, каждой арифметической функции $f(k)$ можно сопоставить последовательность случайных величин $\xi_{n}$ (живущих на разных вероятностных пространствах). Если взять $f(k)=\omega(k)$ (в статье рассуждения проводятся для $f(k)=\Omega(k)$), то несложно, например, показать, что $\mathbb{E}\xi_{n}=\ln\ln n+O(1)$, то есть

$$\sum_{k=1}^{n}\omega(k)=n\ln\ln n+O(n).$$

С дисперсией посложнее, но нетрудно доказать, что $\mathbb{D}\xi_{n}=O(\ln\ln n)$. Применяя неравенство Чебышёва из теории вероятностей, отсюда легко получить теорему Харди–Рамануджана:

$$\mathbb{P}_{n}\left\{\left\lvert\xi_{n}-\mathbb{E}\xi_{n}\right\rvert\geqslant c\right\}\leqslant\frac{\mathbb{D}\xi_{n}}{c^2}\implies\left\lvert\left\{k\leqslant n:\bigl\lvert\omega(k)-\ln\ln n\bigr\rvert\geqslant\sqrt{a(n)\ln\ln n}\right\}\right\rvert=O\left(\frac{n}{a(n)}\right).$$

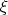
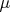
Чтобы изучать предельное распределение, удобно использовать стандартный трюк (как в центральной предельной теореме). Если с.в. $\xi$ имеет нормальное распределение с мат. ожиданием $\mu$ и дисперсией $\sigma^{2}$, то случайная величина $\eta=\frac{\xi-\mu}{\sigma}$ имеет стандартное нормальное распределение (и наоборот). Поэтому вместо последовательности с.в. $\xi_{n}$ удобно рассмотреть «отнормированную» последовательность с.в. $\eta_{n}=\frac{\xi_{n}-\ln\ln n}{\sqrt{\ln\ln n}}$, то есть

$$\eta_{n}(k)=\frac{\omega(k)-\ln\ln n}{\sqrt{\ln\ln n}},\quad1\leqslant k\leqslant n.$$

(Вместо точных значений мат. ожидания и дисперсии используются приближения.) Полученная последовательность отличается от той, которая приведена в Википедии, но она лучше соответствует вероятностному смыслу теоремы (и в статье рассматривается именно она), а формулировку из Википедии можно получить из тех соображений, что $\ln\ln n$ очень медленно меняется, так что $\ln\ln k$ и $\ln\ln n$ — это «почти одно и то же» для «почти всех» $k\in\{1,2,\dotsc,n\}$.

Так вот, теорема Эрдёша–Каца утверждает, что последовательность $\eta_{n}$ слабо сходится к стандартному нормальному распределению, то есть для любого $x\in\mathbb{R}$ выполнено

$$\lim_{n\to\infty}F_{\eta_{n}}(x)=\lim_{n\to\infty}\frac{1}{n}\left\lvert\left\{k\leqslant n:\frac{\omega(k)-\ln\ln n}{\sqrt{\ln\ln n}}\leqslant x\right\}\right\rvert=\Phi(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{x}\mathrm{e}^{-t^{2}/2}\mathrm{d}t.$$

Согласно теореме Леви, это равносильно (поточечной) сходимости для характеристических функций, то есть для произвольного $t\in\mathbb{R}$ верно

$$\lim_{n\to\infty}\varphi_{\eta_{n}}(t)=\lim_{n\to\infty}\frac{1}{n}\sum_{k=1}^{n}\exp\left(\mathrm{i}t\frac{\omega(k)-\ln\ln n}{\sqrt{\ln\ln n}}\right)=\mathrm{e}^{-t^{2}/2}.$$

Последнее предельное соотношение и доказывается в статье (вместе с оценкой скорости сходимости, откуда с помощью неравенства Эссеена получается скорость сходимости в теореме Эрдёша–Каца).

В предельных равенствах

\[\begin{gathered} \lim_{n\to\infty}\frac{1}{n}\left\lvert\left\{k\leqslant n:\frac{\omega(k)-\ln\ln n}{\sqrt{\ln\ln n}}\leqslant x\right\}\right\rvert=\Phi(x),\quad x\in\mathbb{R},\\ \lim_{n\to\infty}\frac{1}{n}\sum_{k=1}^{n}\exp\left(\mathrm{i}t\frac{\omega(k)-\ln\ln n}{\sqrt{\ln\ln n}}\right)=\mathrm{e}^{-t^{2}/2},\quad t\in\mathbb{R}, \end{gathered}\]

Как видите здесь то же вероятностное пространство, что у меня в теме. Обратите внимание на фразу, что произвольную арифметическую функцию (детерминированный объект) можно рассматривать, как случайную величину (стохастический объект). Конечно возникает вопрос, в каком смысле рассматривать?
Далее дается ответ - в смысле создания последовательности случайных величин, у которых значения равны значениям арифметической функции. Поэтому можно говорить о математическом ожидании, дисперсии, функции распределения данной последовательности случайных величин и о предельной функции распределения для последовательности случайных величин.
Именно в этом смысле говорится о предельной функции распределении арифметической функции количества простых делителей натурального числа в теореме Эрдеша-Каца (в данном случае о нормальном распределении), в указанной мною ссылке. Именно в этом смысле я говорю о предельной функции распределения сумматорных арифметических функций Мертенса, Лиувилля и.т.д. у себя в теме.
Для нахождения предельной функции распределения количества простых делителей натурального числа в теореме Эрдеша-Каца, как и во множестве других приложений, используется метод характеристических функций, основанный на теореме Леви о непрерывном соответствии функции распределения и характеристической функции случайной величины. Метод характеристических функций используется и в моей теме для нахождения предельной функции распределения сумматорных арифметических функций.
Утверждения 1 - 4 носят вспомогательный характер. Утверждение 5 является основной теоремой, где используется метод характеристических функций. В данных утверждениях, грубо говоря, доказывается, что при условии асимптотической независимости, ограниченности и определенной степени "измельченности" слагаемых арифметических функций, сумматорная арифметическая функция имеет предельным нормальное распределение. Сравните для примера с центральной предельной теоремой для независимых, одинаково распределенных случайных величин, которая также доказывается методом характеристических функций.

[Lia]

vicvolf в сообщении #1352158 писал(а):

Предположим, что для случайной величины $f_n:f_n(k)=f(k),(n=1,2,...)$ выполняются все условия Утверждения 4

А они выполняются?

Lia в сообщении #1352531 писал(а):

Тогда сумматорная функция, являющаяся частичной суммой данного знакопеременного ряда $S(n)=\sum\limits_{k=1}^{n}{f(k)}=\sum\limits_{k=1}^{n} {a_k+b_k}$

В частичной сумме совсем необязательно поровну положительных и отрицательных слагаемых. Да еще в каждой.

Определение сходимости с.в. по-прежнему отсутствует. По распределению - я вижу, спасибо. Что это такое в Вашем случае?

Отдельный интерес представляет, на каком в.п. задана предельная с.в.

vicvolf в в сообщении #p1352158 писал(а):

$o(n^{-1/2-\epsilon})>>o(1/n)$, (26)

Почему?