Данный текст был задуман как ответ на
претензии monky99. Однако мне эти вычисления быстро надоели. Несколько раз я это бросал, потом возобновлял… В конце-концов, решил всё-таки остановиться на достигнутом и выложить написанное для всеобщего обозрения, согласовав это намерение с
Pphantom. В принципе, найти правильное значение предела координатной скорости в момент достижения горизонта или хотя бы убедиться, что этот предел не равен

, можно было бы и проще, но найти точное решение и прямо на нём показать, что ни о какой

не может быть и речи, кажется более убедительным. Уж что получилось, то и получилось.
I. В координатах Крускала—Секереша метрика шварцшильдовской чёрной дыры имеет вид
От формул (31.14а) и (31.14б) в третьем томе МТУ эти выражения отличаются противоположным знаком метрического тензора и тем, что вместо массы

в качестве параметра используется гравитационный радиус

(в МТУ используется "геометрическая" система единиц, в которой гравитационная постоянная и скорость света равны единице).
Уравнения свободного движения пробной частицы имеют вид

где, в нашем случае,

,

,

,

. Мы будем рассматривать только радиальное движение, поэтому угловые координаты

и

будут иметь постоянные значения; соответственно, мы должны считать, что

и

. При этих условиях вычисления приводят к следующим уравнениям:

К этим уравнениям добавляется ещё одно уравнение, которое получается из выражения (1) "делением" на

; учитывая, что

, и поделив ещё на коэффициент при

, получим

Это уравнение используется для нормировки параметра

; величина

интерпретируется как собственное время движущейся частицы.
Уравнения (3), (4) выглядят сложными, хотя проинтегрировать их в общем виде возможно. Пока рассмотрим вопрос о численном интегрировании. Эти уравнения содержат переменную

, которая связана с

и

уравнением (2). Поскольку явного выражения для

нет, что неудобно для применения численных методов, можно заменить уравнение (2) дифференциальным уравнением. Обозначая

, получим уравнение

, и по формуле производной обратной функции

, откуда по формуле производной сложной функции

Исходные данные выберем такими же, как в
сообщении monky99:

, в начальный момент частица покоится в точке

,

в момент временно́й симметрии координат Крускала—Секереша

; далее из соотношения (2) находим

, из соотношения (5) —

, из соотношения (4) —

.
Далее запускаем Wolfram Mathematica, пишем команду NDSolve (E — основание натуральных логарифмов, \[Pi] — отношение длины окружности к диаметру; откуда взялось выражение

, выяснится позже),
Код:
rg=2;r0=4;v0=0;u0=Sqrt[(r0/rg-1)E^(r0/rg)+v0^2];u10=0;v10=Sqrt[r0/(4rg^3)E^(r0/rg)+u10^2];
SS=NDSolve[{v'[s]==v1[s],u'[s]==u1[s],r'[s]==(2rg^2)/r[s]E^(-(r[s]/rg))(u[s]u1[s]-v[s]v1[s]),
v1'[s]==-(rg/r[s]^2)E^(-(r[s]/rg))(r[s]+rg)(v[s]v1[s]^2-2u[s]v1[s]u1[s]+v[s]u1[s]^2),
u1'[s]==(rg/r[s]^2)E^(-(r[s]/rg))(r[s]+rg)(u[s]v1[s]^2-2v[s]v1[s]u1[s]+u[s]u1[s]^2),
r[0]==r0,v[0]==v0,u[0]==u0,u1[0]==u10,v1[0]==v10},{v,v1,u,u1,r},{s,0,2\[Pi] Sqrt[2]}]
рассчитываем решение и строим на графике мировую линию. Здесь чёрная гипербола сверху — сингулярность, красная прямая — горизонт, зелёная — мировая линия.
Видим, что начальные данные выбраны крайне неудачно: в самой интересной части, где мировая линия пересекает горизонт и утыкается в сингулярность, все три линии сливаются. Поэтому на втором графике изображена небольшая часть вблизи точки пересечения мировой линии и горизонта.
Можно приближённо подобрать момент пересечения горизонта:

(с шестью значащими цифрами); при этом в момент пересечения горизонта

,

,

,

.
На следующих двух графиках показаны зависимости шварцшильдовской радиальной коорданаты

и скорости

от собственного времени падающей частицы.
На левом графике горизонтальная линия изображает горизонт; на правом графике горизонтальная линия изображает скорость света, а вертикальная отмечает момент пересечения горизонта.
Можно подобрать начальные данные, дающие более наглядную картину пересечения горизонта и падения в сингулярность. Возьмём те же самые

,

,

. Далее выбираем

, из соотношения (2) находим

. Значения

и

находим, решая систему уравнений (4) и (5) (подставлено

):

,

. На следующем рисунке изображена не вся мировая линия, а только её конечный участок.
Из этих графиков видна ошибочность утверждений
monky99: в координатах Крускала—Секереша свободно падающая пробная частица "благополучно" пересекает горизонт, имея при этом скорость, меньшую скорости света, и падает в сингулярность. То, что у
monky99 предел скорости при

оказался равным то ли

, то ли

, является следствием банальной ошибки:
нельзя выборочно заменять части выражения их предельными значениями до перехода к пределу.
II. Интегрирование системы уравнений (2), (3), (4) выглядит сложной задачей. Один из способов получить решение состоит в том, чтобы решить задачу для системы координат Шварцшильда, а затем преобразовать его в координаты Крускала—Секереша.
В координатах Шварцшильда метрика имеет вид

где

— скорость света.
Уравнения радиального движения свободного пробного тела имеют вид

 1)
1) Интегрируем первое уравнение системы (7).



Заметим, что вне чёрной дыры направление в будущее соответствует возрастанию

, поэтому должно быть

и, следовательно,

.
2) Интегрируем второе уравнение системы (7). Подставляя в него выражение (9), получим

Принимая в этом уравнении

за новую независимую переменную, а

за новую неизвестную функцию, по формуле производной сложной функции получим

. Подставляя в уравнение, получим

 3)
3) Подставим выражения (9) и (10) в уравнение (8).

Подставляя это значение в (10) и выражая

, получим

В этом уравнении нужно брать знак "

", если при движении тела переменная

увеличивается, и знак "

" — если уменьшается.
4) Из уравнений (9) и (11) по формуле производной функции, заданной параметрически, получаем

Сравнивая это уравнение с уравнением (2.3.5) из книги И. Д. Новикова и В. П. Фролова "Физика чёрных дыр", находим, что

где

— полная энергия частицы, включая её массу покоя

.
5) Интегрируем уравнение (11). Поскольку нас интересует падение частицы в чёрную дыру, перед корнем возьмём знак "

":


(в последнем выражении допущена очень часто встречающаяся вольность: верхний предел интеграла и переменная интегрирования обозначены одной буквой, хотя их смысл совершенно различен).
Для вычисления интеграла сделаем замену переменной:

Подставляем в интеграл:

Вид первообразной здесь существенно зависит от значения

.
5а) Пусть

. Методом Остроградского находим


Возвращаясь к переменной

, получаем
 5б)
5б) Пусть

. Получаем интеграл

Возвращаясь к переменной

, получаем
 5в)
5в) Пусть

. Методом Остроградского находим


Домножая числитель и знаменатель дроби под знаком логарифма на

и возвращаясь к переменной

, получим
 6)
6) Интегрируем уравнение (12). Поскольку нас интересует падение частицы в чёрную дыру, перед корнем возьмём знак "

":


Этот интеграл вычисляется той же подстановкой, что и (14).
6а) 
.
6б) 
.

 6в)
6в) 
.
III. Выше мы рассчитали численно падение частицы в чёрную дыру гравитационного радиуса

с начальными условиями

,

,

,

,

,

,

. Найдём соответствующее точное решение.
Постоянную

находим из уравнения (11), подставляя в него начальные значения:

, откуда

и

.
Комбинируя (14), (15), формулу Ньютона—Лейбница и подставляя заданные значения, получим

Чтобы найти собственное время частицы в момент пересечения горизонта, подставим

; получится

, что совпадает с результатом подбора по численному решению (

) с той точностью, с какой этот подбор выполнен.
Можно также найти собственное время в момент падения в сингулярность: переходя в выражении (22) к пределу при

, получим

(Wolfram Mathematica заканчивает численное интегрирование уравнений движения чуть раньше, с предупреждением "NDSolve::ndsz: At s == 8.885765115903034`, step size is effectively zero; singularity or stiff system suspected.")
Для использования решения (18), (19) нужно найти начальное значение

. Для этого можно использовать формулы перехода от координат Крускала—Секереша к координатам Шварцшильда, которые можно найти в третьем томе МТУ (формулы (31.17а) для области
(I), где

, с учётом изменений в обозначениях):

Подставляя сюда

,

,

,

, найдём
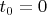
. Подставляя начальные значения,

и

, получим решение

Подставляя выражение (24) в формулы (23) и учитывая, что

,

,

, получим в области
I выражения




Видим, что выражения (25) и (26), определённые для области I, где

, благополучно продолжаются до горизонта

и дают значения

, что совпадает с результатом подбора по численному решению (

) с соответствующей точностью.
Далее нужно продифференцировать выражения (25) и (26). После определённой возни с упрощением громоздких выражений получим

Подставляя в выражение (11) (со знаком "

" перед корнем) значения

и

, получим

теперь по формуле производной сложной функции находим

Наконец, по формуле производной функции, заданной параметрически,

Для сравнения с приближённым решением, найденным численными методами, подставим

в выражения (29) и (30):

,

и

. Все три числа с точностью в шесть значащих цифр совпадают с результатами, полученными численно.
III. Рассмотрим теперь продолжение решения в область
(II), где

, то есть, внутрь чёрной дыры. С выражением (22) никакой проблемы нет, так как оно не имеет никаких особенностей, однако выражение (24) имеет разрыв на горизонте. Проблема в том, что система координат Шварцшильда содержит две карты, никак между собой не связанные: внешнюю (

) и внутреннюю (

). Ни одна из них не содержит точек горизонта

, поэтому невозможно связать решение (24), действующее во внешней области, с каким-либо решением во внутренней области. Чтобы продолжить внешнее решение внутрь чёрной дыры, нужно перейти к координатам, которые не имеют особенностей на горизонте. Внутреннее решение даётся тем же выражением (19), но для определения произвольной постоянной

нельзя использовать определённый интеграл (18). Вместо этого нужно использовать значения внешнего решения на горизонте в качестве начальных значений для внутреннего решения.
В данном случае мы, однако, можем обойтись без этих длинных вычислений. Заметим, что выражения (25)—(29) не имеют никаких особенностей при

; в частности, они удовлетворяют уравнениям (3)—(5) на всём этом интервале. При желании это можно проверить подстановкой в уравнения. Вторые производные по

можно вычислить по формулам

Однако этими длинными вычислениями мы тоже здесь заниматься не будем.
Заметим ещё, что выражение (30) для координатной скорости

при

имеет конечный предел

, в то время как численное решение для

даёт

. Таким образом, даже и в сингулярность частица падает со скоростью, меньшей скорости света.
IV. Выводы. 1) Численное решение очень близко к точному вплоть до момента падения в сингулярность. Поэтому не видно никаких причин не использовать численные методы.
2) Вычисления предела

при

в сообщении
https://dxdy.ru/post1299443.html#p1299443 дало

, а в следующем сообщении
https://dxdy.ru/post1299778.html#p1299778 немного другое вычисление дало

. Я в деталях этих вычислений не копался; типичная причина подобных результатов часто состоит в том, что в одном случае нулями были заменены одни слагаемые, а в другом — другие. Студентов первого курса учат, что заменять в числителе и знаменателе дроби слагаемые их предельными значениями без анализа порядка малости нельзя. Здесь же неожиданно оказывается, что порядки малости некоторых совершенно непохожих выражений (

,

,

) оказываются одинаковыми, поэтому никаким из них пренебрегать нельзя. Правильное значение предела, как мы видели, не равно ни

, ни

, так что падающая частица в координатах Крускала—Шекереса пересекает горизонт событий чёрной дыры с координатной скоростью, меньшей скорости света.
3) Не стоит уделять координатной скорости

слишком много внимания, так как существенного физического смысла она не имеет. В частности, величина этой "скорости" в момент пересечения горизонта или в момент падения в сингулярность существенно зависит от начального значения

, хотя внешняя метрика в координатах Шварцшильда статическая, и падение частицы с любым

выглядит одинаково.