Чтобы найти подход к пониманию того, почему нет натуральных числовых троек удовлетворяющих условию

следует выяснить условия существования пифагоровых троек.
Для этого рассмотрим следующую задачу.
Дана функция

. Для наглядности можно нарисовать её график.
Пусть по оси

от начала координат в положительном направлении отложен отрезок длины

. В момент времени

края отрезка одновременно начинают движение в положительном направлении оси со скоростями: левый край

- со скоростью

, правый край

- со скоростью
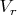
такими, что

(левый край стартовавший из

догоняет правый край стартовавший из

).
Интервал

, имевший в начальный момент времени значение

, будет сокращаться по закону

.
Рассмотрим два события:
1. Момент

, в который квадрат (расстояния пройденного левым краем

) станет равен разности квадрата (расстояния пройденного правым краем

в сумме с начальным интервалом

) и квадрата (начального интервала

):

. Из этого условия найдём значение времени

:

,

 2.
2. Момент

, в который левый край

догонит правый край

:

. Из этого условия найдём значение времени

:


Далее, найдем время прошедшее между этими событиями

:


Из одновременного выполнения условий

следует, что
безразмерно 
Тогда

, откуда


, откуда

что при простом переобозначении:

- начальный интервал

- расстояние пройденное левым краем


- расстояние пройденное правым краем

в сумме с начальным интервалом


- скорость левого края


- скорость правого края

совпадает с хорошо известными заменами членов примитивной пифагоровой тройки:



При этом, условия
1 и
2, из которых были получены итоговые значения, одинаковы для любой исходной функции такой, что

.